26 Nov 2016
To the.. uh, ‘layperson’, pre- and postpromorphisms are probably well into the
WTF category of recursion schemes. This is a mistake - they’re simple and
useful, and I’m going to try and convince you of this in short order.
Preliminaries:
{-# LANGUAGE DeriveFunctor #-}
{-# LANGUAGE LambdaCase #-}
import Data.Functor.Foldable
import Prelude hiding (sum)
For simplicity, let’s take a couple of standard interpreters on lists. We’ll
define ‘sumAlg’ as an interpreter for adding up list contents and ‘lenAlg’ for
just counting the number of elements present:
sumAlg :: Num a => ListF a a -> a
sumAlg = \case
Cons h t -> h + t
Nil -> 0
lenAlg :: ListF a Int -> Int
lenAlg = \case
Cons h t -> 1 + t
Nil -> 0
Easy-peasy. We can use cata to make these
things useful:
sum :: Num a => [a] -> a
sum = cata sumAlg
len :: [a] -> Int
len = cata lenAlg
Nothing new there; ‘sum [1..10]’ will give you 55 and ‘len [1..10]’ will give
you 10.
An interesting twist is to consider only small elements in some sense; say,
we only want to add or count elements that are less than or equal to 10, and
ignore any others.
We could rewrite the previous interpreters, manually checking for the condition
we’re interested in and handling it accordingly:
smallSumAlg :: (Ord a, Num a) => ListF a a -> a
smallSumAlg = \case
Cons h t ->
if h <= 10
then h + t
else 0
Nil -> 0
smallLenAlg :: (Ord a, Num a) => ListF a Int -> Int
smallLenAlg = \case
Cons h t ->
if h <= 10
then 1 + t
else 0
Nil -> 0
And you get ‘smallSum’ and ‘smallLen’ by using ‘cata’ on them respectively.
They work like you’d expect - ‘smallLen [1, 5, 20]’ ignores the 20 and just
returns 2, for example.
You can do better though. Enter the prepromorphism.
Instead of writing additional special-case interpreters for the ‘small’ case,
consider the following natural transformation on the list base functor. It
maps the list base functor to itself, without needing to inspect the carrier
type:
small :: (Ord a, Num a) => ListF a b -> ListF a b
small Nil = Nil
small term@(Cons h t)
| h <= 10 = term
| otherwise = Nil
A prepromorphism is a ‘cata’-like recursion scheme that proceeds by first
applying a natural transformation before interpreting via a supplied algebra.
That’s.. surprisingly simple. Here are ‘smallSum’ and ‘smallLen’, defined
without needing to clumsily create new special-case algebras:
smallSum :: (Ord a, Num a) => [a] -> a
smallSum = prepro small sumAlg
smallLen :: (Ord a, Num a) => [a] -> Int
smallLen = prepro small lenAlg
They work great:
> smallSum [1..100]
55
> smallLen [1..100]
10
In pseudo category-theoretic notation you visualize how a prepromorphism works
via the following commutative diagram:
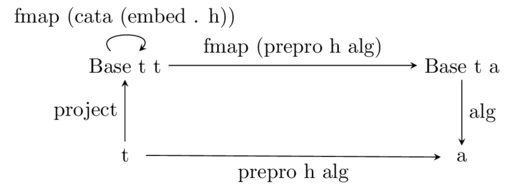
The only difference, when compared to a standard
catamorphism, is the presence of the natural
transformation applied via the looping arrow in the top left. The natural
transformation ‘h’ has type ‘forall r. Base t r -> Base t r’, and ‘embed’ has
type ‘Base t t -> t’, so their composition gets you exactly the type you need
for an algebra, which is then the input to ‘cata’ there. Mapping the
catamorphism over the type ‘Base t t’ brings it right back to ‘Base t t’.
A postpromorphism is dual to a prepromorphism. It’s ‘ana’-like; proceed with
your corecursive production, applying natural transformations as you go.
Here’s a streaming coalgebra:
streamCoalg :: Enum a => a -> ListF a a
streamCoalg n = Cons n (succ n)
A normal anamorphism would just send this thing shooting off into infinity, but
we can use the existing ‘small’ natural transformation to cap it at 10:
smallStream :: (Ord a, Num a, Enum a) => a -> [a]
smallStream = postpro small streamCoalg
You get what you might expect:
> smallStream 3
[3,4,5,6,7,8,9,10]
And similarly, you can visualize a postpromorphism like so:
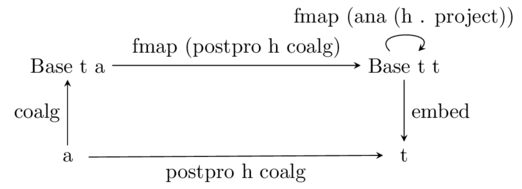
In this case the natural transformation is applied after mapping the
postpromorphism over the base functor (hence the ‘post’ namesake).
26 Oct 2016
Some time ago I came across a way to in-principle perform inference on certain
probabilistic programs using comonadic structures and operations.
I decided to dig it up and try to use it to extend the simple probabilistic
programming language I talked about a few days ago with a stateful,
experimental inference backend. In this post we’ll
- Represent probabilistic programs as recursive types parameterized by
a terminating instruction set.
- Represent execution traces of probabilistic programs via a simple
transformation of our program representation.
- Implement the Metropolis-Hastings algorithm over this space of execution
traces and thus do some inference.
Let’s get started!
Representing Programs That Terminate
I like thinking of embedded languages in terms of instruction sets. That is:
I want to be able to construct my embedded language by first defining a
collection of abstract instructions and then using some appropriate recursive
structure to represent programs over that set.
In the case of probabilistic programs, our instructions are probability
distributions. Last time we used the following simple instruction set to
define our embedded language:
data ModelF r =
BernoulliF Double (Bool -> r)
| BetaF Double Double (Double -> r)
deriving Functor
We then created an embedded language by just wrapping it up in the
higher-kinded Free type to denote programs of type Model.
data Free f a =
Pure a
| Free (f (Free f a))
type Model = Free ModelF
Recall that Free represents programs that can terminate, either by some
instruction in the underlying instruction set, or via the Pure constructor of
the Free type itself. The language defined by Free ModelF is expressive
enough to easily construct a ‘forward-sampling’ interpreter, as well as a
simple rejection sampler for performing inference.
Notice that we don’t have a terminating instruction in ModelF itself - if
we’re using it, then we need to rely on the Pure constructor of Free to
terminate programs. Otherwise they’d just have to recurse forever. This can
be a bit limiting if we want to transform a program of type Free ModelF to
something else that doesn’t have a notion of termination baked-in (Fix, for
example).
Let’s tweak the ModelF type to get the following:
data ModelF a r =
BernoulliF Double (Bool -> r)
| BetaF Double Double (Double -> r)
| NormalF Double Double (Double -> r)
| DiracF a
deriving Functor
Aside from adding another foundational distribution - NormalF - we’ve also
added a new constructor, DiracF, which carries a parameter with type a. We
need to incorporate this carrier type in the overall type of ModelF as well,
so ModelF itself also gets a new type parameter to carry around.
The DiracF instruction is a terminating instruction; it has no recursive
point and just terminates with a value of type a when reached. It’s
structurally equivalent to the Pure a branch of Free that we were relying
on to terminate our programs previously - the only thing we’ve done is add it
to our instruction set proper.
Why DiracF? A Dirac distribution places the entirety of its
probability mass on a single point, and this is the exact probabilistic
interpretation of the applicative pure or monadic return that one
encounters with an appropriate probability type. Intuitively, if I sample a
value \(x\) from a uniform distribution, then that is indistinguishable from
sampling \(x\) from said uniform distribution and then sampling from a Dirac
distribution with parameter \(x\).
Make sense? If not, it might be helpful to note that there is no difference
between any of the following (to which uniform and dirac are analogous):
> action :: m a
> action >>= return :: m a
> action >>= return >>= return >>= return :: m a
Wrapping ModelF a up in Free, we get the following general type for our
programs:
type Program a = Free (ModelF a)
And we can construct a bunch of embedded language terms in the standard way:
beta :: Double -> Double -> Program a Double
beta a b = liftF (BetaF a b id)
bernoulli :: Double -> Program a Bool
bernoulli p = liftF (BernoulliF p id)
normal :: Double -> Double -> Program a Double
normal m s = liftF (NormalF m s id)
dirac :: a -> Program a b
dirac x = liftF (DiracF x)
Program is a general type, capturing both terminating and nonterminating
programs via its type parameters. What do I mean by this? Note that in
Program a b, the a type parameter can only be concretely instantiated via
use of the terminating dirac term. On the other hand, the b type parameter
is unaffected by the dirac term; it can only be instantiated by the other
nonterminating terms: beta, bernoulli, normal, or compound expressions of
these.
We can thus distinguish between terminating and nonterminating programs at the
type level, like so:
type Terminating a = Program a Void
type Model b = forall a. Program a b
Void is the uninhabited type, brought into scope via Data.Void or simply
defined via data Void = Void Void. Any program that ends via a dirac
instruction must be Terminating, and any program that doesn’t end with a
dirac instruction can not be Terminating. We’ll just continue to call
a nonterminating program a Model, as before.
Good. So if it’s not clear: from a user’s perspective, nothing has changed.
We still write probabilistic programs using simple monadic language terms.
Here’s a Gaussian mixture model where the mixing parameter follows a beta
distribution, for example:
mixture :: Double -> Double -> Model Double
mixture a b = do
prob <- beta a b
accept <- bernoulli prob
if accept
then normal (negate 2) 0.5
else normal 2 0.5
Meanwhile the syntax tree generated looks something like the following. It’s
more or less a traditional probabilistic graphical model description of our
program:
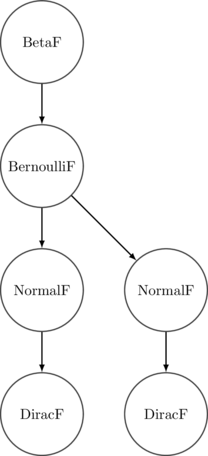
It’s important to note that in this embedded framework, the only pieces of the
syntax tree that we can observe are those related directly to our primitive
instructions. For our purposes this is excellent - we can focus on programs
entirely at the level of their probabilistic components, and ignore the
deterministic parts that would otherwise be distractions.
To collect samples from mixture, we can first interpret it into a sampling
function, and then simulate from it. The toSampler function from last
time doesn’t change much:
toSampler :: Program a a -> Prob IO a
toSampler = iterM $ \case
BernoulliF p f -> Prob.bernoulli p >>= f
BetaF a b f -> Prob.beta a b >>= f
NormalF m s f -> Prob.normal m s >>= f
DiracF x -> return x
Sampling from mixture 2 3 a thousand times yields the following
> simulate (toSampler (mixture 2 3))
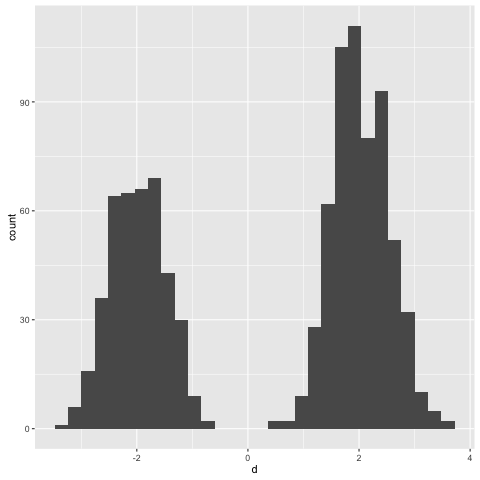
Note that the rightmost component gets more traffic due to the hyperparameter
combination of 2 and 3 that we provided to mixture.
Also, a note - since we have general recursion in Haskell, so-called
‘terminating’ programs here can actually.. uh, fail to terminate. They must
only terminate as far as we can express the sentiment at the embedded language
level. Consider the following, for example:
foo :: Terminating a
foo = (loop 1) >>= dirac where
loop a = do
p <- beta a 1
loop p
foo here doesn’t actually terminate. But at least this kind of weird case
can be picked up in the types:
> :t simulate (toSampler foo)
simulate (toSampler foo) :: IO Void
If you try to sample from a distribution over Void or forall a. a then I
can’t be held responsible for what you get up to. But there are other cases,
sadly, where we’re also out of luck:
trollGeometric :: Double -> Model Int
trollGeometric p = loop where
loop = do
accept <- return False
if accept
then return 1
else fmap succ loop
A geometric distribution that actually used its argument \(p\), for \(0 < p
\leq 1\), could be guaranteed to terminate with probability 1. This one
doesn’t, so trollGeometric undefined >>= dirac won’t.
At the end of the day we’re stuck with what our host language offers us. So,
take the termination guarantees for our embedded language with a grain of salt.
Stateful Inference
In the previous post we used a simple rejection sampler to sample from
a conditional distribution. ‘Vanilla’ Monte Carlo algorithms like rejection
and importance sampling are stateless. This makes them nice in some ways -
they tend to be simple to implement and are embarrassingly parallel, for
example. But the curse of dimensionality prevents them from scaling
well to larger problems. I won’t go into detail on that here - for a deep dive
on the topic, you probably won’t find anything better than this phenomenal
couple of talks on MCMC that Iain Murray gave at a MLSS session in
Cambridge in 2009. I think they’re unparalleled to this day.
The point is that in higher dimensions we tend to get a lot out of state.
Essentially, if one finds an interesting region of high-dimensional parameter
space, then it’s better to remember where that is, rather than forgetting it
exists as soon as one stumbles onto it. The manifold hypothesis conjectures
that interesting regions of space tend to be near other interesting regions
of space, so exploring neighbourhoods of interesting places tends to pay off.
Stateful Monte Carlo methods - namely, the family of Markov chain Monte Carlo
algorithms - handle exactly this, by using a Markov chain to wander over
parameter space. I’ve written on MCMC in the past -
you can check out some of those articles if you’re interested.
In the stateless rejection sampler we just performed conditional inference via
the following algorithm:
- Sample from a parameter model.
- Sample from a data model, using the sample from the parameter model as
input.
- If the sample from the data model matches the provided observations, return
the sample from the parameter model.
By repeating this many times we get a sample of arbitrary size from the
appropriate conditional, inverse, or posterior distribution (whatever you want
to call it).
In a stateful inference routine - here, the good old Metropolis-Hastings
algorithm - we’re instead going to do the following repeatedly:
- Sample from a parameter model, recording the way the program executed in
order to return the sample that it did.
- Compute the cost, in some sense, of generating the provided observations,
using the sample from the parameter model as input.
- Propose a new sample from the parameter model by perturbing the way the
program executed and recording the new sample the program outputs.
- Compute the cost of generating the provided observations using this new
sample from the parameter model as input.
- Compare the costs of generating the provided observations under the
respective samples from the parameter models.
- With probability depending on the ratio of the costs, flip a coin. If you
see a head, then move to the new, proposed execution trace of the program.
Otherwise, stay at the old execution trace.
This procedure generates a Markov chain over the space of possible execution
traces of the program - essentially, plausible ways that the program could have
executed in order to generate the supplied observations.
Implementations of Church use variations of this method to do
inference, the most famous of which is a low-overhead transformational
compilation procedure described in a great and influential 2011 paper
by David Wingate et al.
Representing Running Programs
To perform inference on probabilistic programs according to the aforementioned
Metropolis-Hastings algorithm, we need to represent executing programs
somehow, in a form that enables us to examine and modify their internal state.
How can we do that? We’ll pluck another useful recursive structure from our
repertoire and consider the humble Cofree:
data Cofree f a = a :< f (Cofree f a)
Recall that Cofree allows one to annotate programs with arbitrary
information at each internal node. This is a great feature; if we can annotate
each internal node with important information about its state - its current
value, the current state of its generator, the ‘cost’ associated with it - then
we can walk through the program and examine it as required. So, it can capture
a ‘running’ program in exactly the way we need.
Let’s describe running programs as values having the following Execution
type:
type Execution a = Cofree (ModelF a) Node
The Node type is what we’ll use to describe the internal state of each node
on the program. I’ll define it like so:
data Node = Node {
nodeCost :: Double
, nodeValue :: Dynamic
, nodeSeed :: MWC.Seed
, nodeHistory :: [Dynamic]
} deriving Show
I’ll elaborate on this type below, but you can see that it captures a bunch of
information about the state of each node.
One can mechanically transform any Free-encoded program into a
Cofree-encoded program, so long as the original Free-encoded program can
terminate of its own accord, i.e. on the level of its own instructions. Hence
the need for our Terminating type and all that.
In our case, setting everything up just right takes a bit of code, mainly
around handling pseudo-random number generators in a pure fashion. So
I won’t talk about every little detail of it right here. The general idea is
to write a function that takes instructions to the appropriate state captured
by a Node value, like so:
initialize :: Typeable a => MWC.Seed -> ModelF a b -> Node
initialize seed = \case
BernoulliF p _ -> runST $ do
(nodeValue, nodeSeed) <- samplePurely (Prob.bernoulli p) seed
let nodeCost = logDensityBernoulli p (unsafeFromDyn nodeValue)
nodeHistory = mempty
return Node {..}
BetaF a b _ -> runST $ do
(nodeValue, nodeSeed) <- samplePurely (Prob.beta a b) seed
let nodeCost = logDensityBeta a b (unsafeFromDyn nodeValue)
nodeHistory = mempty
return Node {..}
...
You can see that for each node, I sample from it, calculate its cost, and then
initialize its ‘history’ as an empty list.
Here it’s worth going into a brief aside.
There are two mildly annoying things we have to deal with in this situation.
First, individual nodes in the program typically sample values at different
types, and second, we can’t easily use effects when annotating. This means
that we have to pack heterogeneously-typed things into a homogeneously-typed
container, and also use pure random number generation facilities to sample
them.
A quick-and-dirty answer for the first case is to just use dynamic typing when
storing the values. It works and is easy, but of course is subject to the
standard caveats. I use a function called unsafeFromDyn to convert
dynamically-typed values back to a typed form, so you can gauge the safety of
all this for yourself.
For the second case, I just use the ST monad, along with manual state
snapshotting, to execute and iterate a random number generator. Pretty
simple.
Also: in terms of efficiency, keeping a node’s history on-site at each
execution falls into the ‘completely insane’ category, but let’s not worry much
about efficiency right now. Prototypes gonna prototype and all that.
Anyway.
Given this initialize function, we can transform a terminating program into a
running program by simple recursion. Again, we can only transform programs
with type Terminating a because we need to rule out the case of ever visiting
the Pure constructor of Free. We handle that by the absurd function
provided by Data.Void:
execute :: Typeable a => Terminating a -> Execution a
execute = annotate defaultSeed where
defaultSeed = (42, 108512)
annotate seeds term = case term of
Pure r -> absurd r
Free instruction ->
let (nextSeeds, generator) = xorshift seeds
seed = MWC.toSeed (V.singleton generator)
node = initialize seed instruction
in node :< fmap (annotate nextSeeds) instruction
And there you have it - execute takes a terminating program as input and
returns a running program - an execution trace - as output. The syntax tree we
had previously gets turned into something like this:
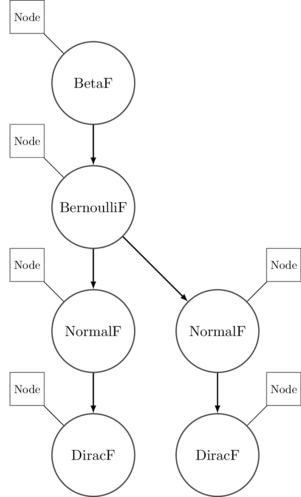
Perturbing Running Programs
Given an execution trace, we’re able to step through it sequentially and
investigate the program’s internal state. But to do inference we also need to
modify it as well. What’s the answer here?
Just as Free has a monadic structure that allows us to write embedded
programs using built-in monadic combinators and do-notation, Cofree has a
comonadic structure that is amenable to use with the various comonadic
combinators found in Control.Comonad. The most important for our purposes is
the comonadic ‘extend’ operation that’s dual to monad’s ‘bind’:
extend :: Comonad w => (w a -> b) -> w a -> w b
extend f = fmap f . duplicate
To perturb a running program, we can thus write a function that perturbs any
given annotated node, and then extend it over the entire execution trace.
The perturbNode function can be similar to the initialize function from
earlier; it describes how to perturb every node based on the instruction found
there:
perturbNode :: Execution a -> Node
perturbNode (node@Node {..} :< cons) = case cons of
BernoulliF p _ -> runST $ do
(nvalue, nseed) <- samplePurely (Prob.bernoulli p) nodeSeed
let nscore = logDensityBernoulli p (unsafeFromDyn nvalue)
return $! Node nscore nvalue nseed nodeHistory
BetaF a b _ -> runST $ do
(nvalue, nseed) <- samplePurely (Prob.beta a b) nodeSeed
let nscore = logDensityBeta a b (unsafeFromDyn nvalue)
return $! Node nscore nvalue nseed nodeHistory
...
Note that this is a very crude way to perturb nodes - we’re just sampling from
whatever distribution we find at each one. A more refined procedure would
sample from each node on a more local basis, sampling from its respective
domain in a neighbourhood of its current location. For example, to perturb a
BetaF node we might sample from a tiny Gaussian bubble around its current
location, repeating the process if we happen to ‘fall off’ the support. I’ll
leave matters like that for another post.
Perturbing an entire trace is then as easy as I claimed it to be:
perturb :: Execution a -> Execution a
perturb = extend perturbNode
For some comonadic intuition: when we ‘extend’ a function over an execution,
the trace itself gets ‘duplicated’ in a comonadic context. Each node in the
program becomes annotated with a view of the rest of the execution trace from
that point forward. It can be difficult to visualize at first, but I reckon
the following image is pretty faithful:

Each annotation then has perturbNode applied to it, which reduces the trace
back to the standard annotated version we saw before.
Iterating the Markov Chain
So: to move around in parameter space, we’ll propose state changes by
perturbing the current state, and then accept or reject proposals according to
local economic conditions.
If you already have no idea what I’m talking about, then the phrase ‘local
economic conditions’ probably didn’t help you much. But it’s a useful analogy
to have in one’s head. Each state in parameter space has a cost associated
with it - the cost of generating the observations that we’re conditioning on
while doing inference. If certain parameter values yield a data model that is
unlikely to generate the provided observations, then those observations will be
expensive to generate when measured in terms of log-likelihood. Parameter
values that yield data models more likely to generate the supplied observations
will be comparatively cheaper.
If a proposed execution trace is significantly cheaper than the trace we’re
currently at, then we usually want to move to it. We allow some randomness in
our decision to keep everything nice and measure-preserving.
We can thus construct the conditional distribution over execution traces using
the following invert function, using the same nomenclature as the rejection
sampler we used previously. To focus on the main points, I’ll elide some of
its body:
invert
:: (Eq a, Typeable a, Typeable b)
=> Int -> [a] -> Model b -> (b -> a -> Double)
-> Model (Execution b)
invert epochs obs prior ll = loop epochs (execute terminated) where
terminated = prior >>= dirac
loop n current
| n == 0 = return current
| otherwise = do
let proposal = perturb current
-- calculate costs and movement probability here
accept <- bernoulli prob
let next = if accept then proposal else stepGenerators current
loop (pred n) (snapshot next)
There are a few things to comment on here.
First, notice how the return type of invert is Model (Execution b)? Using
the semantics of our embedded language, it’s literally a standard model over
execution traces. The above function returns a first-class value that is
completely uninterpreted and abstract. Cool.
We’re also dealing with things a little differently from the rejection sampler
that we built previously. Here, the data model is expressed by a cost
function; that is, a function that takes a parameter value and observation as
input, and returns the cost of generating the observation (conditional on the
supplied parameter value) as output. This is the approach used in the
excellent Practical Probabilistic Programming with Monads paper by Adam
Scibior et al and also mentioned by Dan Roy in his recent talk at the
Simons Institute. Ideally we’d just reify the cost function here from the
description of a model directly (to keep the interface similar to the one used
in the rejection sampler implementation), but I haven’t yet found a way to do
this in a type-safe fashion.
Regardless of whether or not we accept a proposed move, we need to snapshot the
current value of each node and add it to that node’s history. This can be done
using another comonadic extend:
snapshotValue :: Cofree f Node -> Node
snapshotValue (Node {..} :< cons) = Node { nodeHistory = history, .. } where
history = nodeValue : nodeHistory
snapshot :: Functor f => Cofree f Node -> Cofree f Node
snapshot = extend snapshotValue
The other point of note is minor, but an extremely easy detail to overlook.
Since we’re handling random value generation at each node purely, using on-site
PRNGs, we need to iterate the generators forward a step in the event that we
don’t accept a proposal. Otherwise we’d propose a new execution based on the
same generator states that we’d used previously! For now I’ll just iterate the
generators by forcing a sample of a uniform variate at each node, and then
throwing away the result. To do this we can use the now-standard comonadic
pattern:
stepGenerator :: Cofree f Node -> Node
stepGenerator (Node {..} :< cons) = runST $ do
(nval, nseed) <- samplePurely (Prob.beta 1 1) nodeSeed
return Node {nodeSeed = nseed, ..}
stepGenerators :: Functor f => Cofree f Node -> Cofree f Node
stepGenerators = extend stepGenerator
Inspecting Execution Traces
Alright so let’s see how this all works. Let’s write a model, condition it
on some observations, and do inference.
We’ll choose our simple Gaussian mixture model from earlier, where the mixing
probability follows a beta distribution, and cluster assignment itself follows
a Bernoulli distribution. We thus choose the ‘leftmost’ component of the
mixture with the appropriate mixture probability.
We can break the mixture model up as follows:
prior :: Double -> Double -> Model Bool
prior a b = do
p <- beta a b
bernoulli p
likelihood :: Bool -> Model Double
likelihood left
| left = normal (negate 2) 0.5
| otherwise = normal 2 0.5
Let’s take a look at some samples from the marginal distribution. This time
I’ll flip things and assign hyperparameters of 3 and 2 for the prior:
> simulate (toSampler (prior 3 2 >>= likelihood))
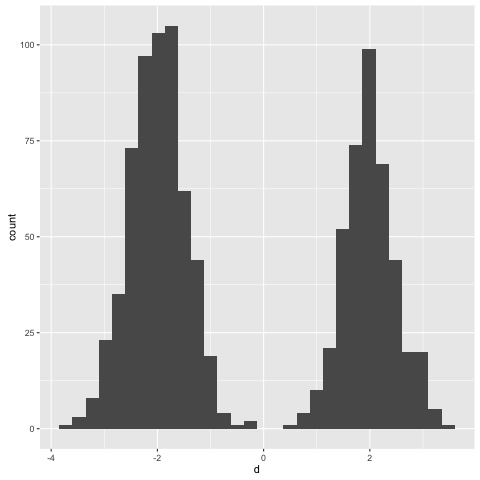
It looks like we’re slightly more likely to sample from the left mixture
component than the right one. Again, this makes sense - the mean of a beta(3,
2) distribution is 0.6.
Now, what about inference? I’ll define the conditional model as follows:
posterior :: Model (Execution Bool)
posterior = invert 1000 obs prior ll where
obs = [ -1.7, -1.8, -2.01, -2.4
, 1.9, 1.8
]
ll left
| left = logDensityNormal (negate 2) 0.5
| otherwise = logDensityNormal 2 0.5
Here we have four observations that presumably arise from the leftmost
component, and only two that match up with the rightmost. Note also that I’ve
replaced the likelihood model with its appropriate cost function due to
reasons I mentioned in the last section. (It would be easy to reify this
model as its cost function, but doing it for general models is trickier)
Anyway, let’s sample from the conditional distribution:
> simulate (toSampler posterior)
Sampling returns a running program, of course, and we can step through it to
examine its structure. We can use the supplied values recorded at each node
to ‘automatically’ step through execution, or we can supply our own values to
investigate arbitrary branches.
The conditional distribution we’ve found over the mixing probability is as
follows:
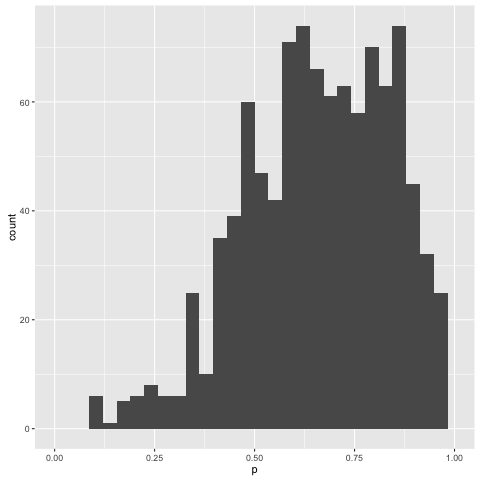
Looks like we’re in the right ballpark.
We can examine the traces of other elements of the program as well. Here’s the
recorded distribution over component assignments, for example - note that the
rightmost bar here corresponds to the leftmost component in the mixture:
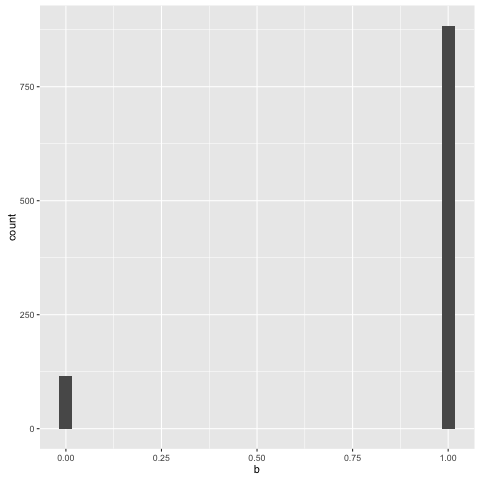
You can see that whenever we wandered into the rightmost component, we’d
swiftly wind up jumping back out of it:
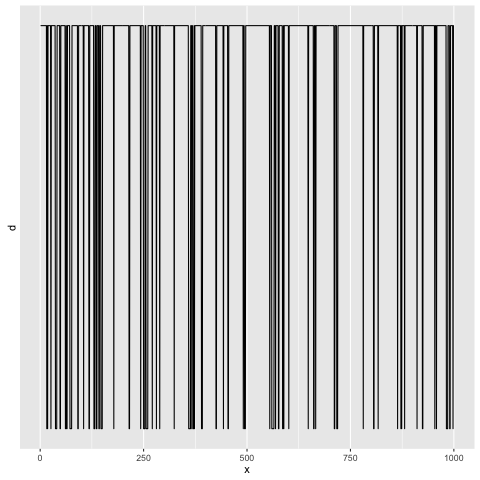
This is a fun take on probabilistic programming. In particular I find a few
aspects of the whole setup to be pretty attractive:
We use a primitive, limited instruction set to parameterize both programs - via
Free - and running programs - via Cofree. These off-the-shelf recursive
types are used to wrap things up and provide most of our required control flow
automatically. It’s easy to transparently add structure to embedded programs
built in this way; for example, we can statically encode independence
by replacing our ModelF a type with something like:
data InstructionF a = Coproduct (ModelF a) (Ap (ModelF a))
This can be hidden from the user so that we’re left with the same simple
monadic syntax we presently enjoy, but we also get to take independence into
account when performing inference, or any other structural interpretation for
that matter.
When it comes to inference, the program representation is completely separate
from whatever inference backend we choose to augment it with. We can deal with
traces as first-class values that can be directly stored, inspected,
manipulated, and so on. And everything is done in a typed and
purely-functional framework. I’ve used dynamic typing functionality from
Data.Dynamic to store values in execution traces here, but we could similarly
just define a concrete Value type with the appropriate constructors for
integers, doubles, bools, etc., and use that to store everything.
At the same time, this is a pretty early concept - doing inference
efficiently in this setting is another matter, and there are a couple of
computational and statistical issues here that need to be ironed out to make
further progress.
The current way I’ve organized Markov chain generation and iteration is just
woefully inefficient. Storing the history of each node on-site is needlessly
costly and I’m sure results in a ton of unnecessary allocation. On a semantic
level, it also ‘complects’ state and identity: why, after all, should a single
execution trace know anything about traces that preceded it? Clearly this
should be accumulated in another data structure. There is a lot of other
low-hanging fruit around strictness and PRNG management as well.
From a more statistical angle, the present implementation does a poor job when
it comes to perturbing execution traces. Some changes - such as improving the
proposal mechanism for a given instruction - are easy to implement, and
representing distributions as instructions indeed makes it easy to tailor local
proposal distributions in a context-independent way. But another problem is
that, by using a ‘blunt’ comonadic extend, we perturb an execution by
perturbing every node in it. In general it’s better to make small
perturbations rather than large ones to ensure a reasonable acceptance ratio,
but to do that we’d need to perturb single nodes (or at least subsets of nodes)
at a time.
There may be some inroads here via comonad transformers like StoreT or
lenses that would allow us to zoom in on a particular node and perturb it,
rather than perturbing everything at once. But my comonad-fu is not yet quite
at the required level to evaluate this, so I’ll come back to that idea some
other time.
I’m interested in playing with this concept some more in the future, though I’m
not yet sure how much I expect it to be a tenable way to do inference at scale.
If you’re interested in playing with it, I’ve dumped the code from this post
into this gist.
Thanks to Niffe Hermansson and Fredrik Olsen for reviewing a draft of this
post and providing helpful comments.









