Randomness in Haskell

01 Oct 2016

Randomness is a constant nuisance point for Haskell beginners who may be coming from a language like Python or R. While in Python you can just get away with something like:

In [2]: numpy.random.rand(3)
Out[2]: array([ 0.61426175,  0.05309224,  0.38861597])

or in R:

> runif(3)
[1] 0.49473012 0.68436352 0.04135914

In Haskell, the situation is more complicated. It’s not too much worse when you get the hang of things, but it’s certainly one of those things that throws beginners for a loop - and for good reason.

In this article I want to provide a simple guide, with examples, for getting started and becoming comfortable with randomness in Haskell. Hopefully it helps!

I’m writing this from a hotel during my girlfriend’s birthday, so it’s being slapped together very rapidly with a kind of get-it-done attitude. If anything is unclear or you have any questions, feel free to shoot me a ping and I’ll try to improve it when I get a chance.

Randomness on Computers in General

Check out the R code I posted previously. If you just open R and type runif(3) on your machine, then odds are you’ll get a different triple of numbers than what I got above.

These numbers are being generated based on R’s global random number generator (RNG), which, absent any fiddling by the user, is initialized as needed based on the system time and ID of the R process. So: if you open up the R interpreter and call runif(3), then behind the scenes R will initialize the RNG based on the time and process ID, and then use a particular algorithm to generate random numbers based on that initialized value (called the ‘seed’).

These numbers aren’t truly random - they’re pseudo-random, which means they’re generated by a deterministic algorithm such that the resulting values appear random over time. The default algorithm used by R, for example, is the famous Mersenne Twister, which you can verify as follows:

> RNGkind()
[1] "Mersenne-Twister" "Inversion"

You can also set the seed yourself in R, using the set.seed function. Then if you type something like runif(3), R will use this initialized RNG rather than coming up with its own seed based on the time and process ID. Setting the seed allows you to reproduce operations involving pseudo-random numbers; just re-set the seed and perform the same operations again:

> set.seed(42)
> runif(3)
[1] 0.9148060 0.9370754 0.2861395
> set.seed(42)
> runif(3)
[1] 0.9148060 0.9370754 0.2861395

(It’s good practice to always initialize the RNG using some known seed before running an experiment, simulation, and so on.)

So the big thing to notice here, in any case, is that R uses a global RNG. It maintains the state of this RNG implicitly and behind the scenes. When you type runif(3), R consults this implicit RNG, gives you your pseudo-random numbers based on its value, and updates the global RNG without you needing to worry about any of this plumbing yourself. The same is generally true for randomness in most programming languages - Python, C, Ruby, and so on.

Explicit RNG Management

But let’s come back to Haskell. Haskell, unlike R or Python, is purely-functional. State, or effects in general, are never implicit in the same way that R updates its global RNG. We need to either explicitly pass around a RNG ourselves, or at least allow some explicit monad to do it for us.

Passing around a RNG manually is annoying, so in practice this means everyone uses a monad to handle RNG state. This means that one needs to be comfortable working with monadic code in order to practically use random numbers in Haskell, which presents a big hurdle for beginners who may have been able to ignore monads thus far on their Haskell journey.

Let’s see what I mean by all of this by going through a few examples. Make sure you have stack installed, and then grab a few libraries that we’ll make use of in the remainder of this post:

$ stack install random mwc-random primitive

The Really Annoying Method - Manual RNG Management

Let me demonstrate the simplest conceptual method for dealing with random numbers: manually grabbing and passing around a RNG without involving any monads whatsoever.

First, open up GHCi:

$ stack ghci

And let’s also get some quick preliminaries out of the way:

Prelude> :set prompt "> "
> import System.Random
> import Control.Monad
> let runif_pure = randomR (0 :: Double, 1)
> let runif n = replicateM n (randomRIO (0 :: Double, 1))
> let set_seed = setStdGen . mkStdGen

We’ll first use the basic System.Random module for illustration. To initialize a RNG, we can make one by providing the mkStdGen function with an integer seed:

> let rng = mkStdGen 42
> rng
43 1

We can use this thing to generate random numbers. A simple function to do that is randomR, which will generate pseudo-random values for some ordered type in a given range. We’ll use the runif_pure alias for it that we defined previously, just to make things look similar to the previous R example and also emphasize that this one is a pure function:

> runif_pure rng
(1.0663729393723398e-2,2060101257 2103410263)

You can see that we got back a pair of values, the first element of which is our random number 1.0663729393723398e-2. Cool. Let’s try to generate another:

> runif_pure rng
(1.0663729393723398e-2,2060101257 2103410263)

Hmm. We generated the same number again. This is because the value of rng hasn’t changed - it’s still the same value we made via mkStdGen 42. Since we’re using the same random number generator to generate a pseudo-random value, we get the same pseudo-random value.

If we want to make new random numbers, then we need to use a different generator. And the second element of the pair returned from our call to runif_pure is exactly that - an updated RNG that we can use to generate additional random numbers.

Let’s try that all again, using the generator we get back from the first function call as an input to the second:

> let (x, rng1) = runif_pure rng
> x
1.0663729393723398e-2
> let (y, rng2) = runif_pure rng1
> y
0.9827538369038856

Success!

I mean.. sort of. It works and all, and it does constitute a general-purpose solution. But manually binding updated RNG states to names and swapping those in for new values is still pretty annoying.

You could also generate an infinite list of random numbers using the randomRs function and just take from it as needed, but you still probably need to manage that list to make sure you don’t re-use any numbers. You kind of trade off managing the RNG for managing an infinite list of random numbers, which isn’t much better.

The Less-Annoying Method - Get A Monad To Do It

The good news is that we can offload the job of managing the RNG state to a monad. I won’t actually explain how that works in detail here - I think most people facing this problem are initially more concerned with getting something working, rather than deeply grokking monads off the bat - so I’ll just claim that we can get a monad to handle the RNG state for us, and that will hopefully (mostly) suffice for now.

Still rolling with the System.Random module for the time being, we’ll use the runif alias for the randomRIO function that we defined previously to generate some new random numbers:

> runif 3
[0.9873934690803106,0.3794382930121829,0.2285653405908732]
> runif 3
[0.7651878964537555,0.2623159001635825,0.7683468476766804]

Simpler! Notice we haven’t had to do anything with a generator manually - we just ask for random numbers and then get them, just like in R. And if we want to set the value of the RNG being used here, we can use the setStdGen function with an RNG that we’ve already created. Here let’s just use the set_seed alias we defined earlier, to mimic R’s set.seed function:

> set_seed 42
> runif 3
[1.0663729393723398e-2,0.9827538369038856,0.7042944187434987]
> set_seed 42
> runif 3
[1.0663729393723398e-2,0.9827538369038856,0.7042944187434987]

So things are similar to how they work in R here - we have a global RNG of sorts, and we can set its state as desired using the set_seed function. But since this is Haskell, the effects of creating and updating the generator state must still be explicit. And they are explicit - it’s just that they’re explicit in the type of runif:

> :t runif
runif :: Int -> IO [Double]

Note that runif returns a value that’s wrapped up in IO. This is how we indicate explicitly - at the type level - that something is being done with the generator in the background. IO is a monad, and it happens to be the thing that’s dealing with the generator for us here.

What this means for you, the practitioner, is that you can’t just mix values of some type a with values of type IO a willy-nilly. You may be writing a function f with type [Double] -> Double, where the input list of doubles is intended to be randomly-generated. But if you just go ahead and generate a list xs of random numbers, they’ll have type IO [Double], and you’ll stare in confusion at some type error from GHC when you try to apply f to xs.

Here’s what I mean. Take the example of just generating some random numbers and then summing them up. First, in R:

> xs = runif(3)
> sum(xs)
[1] 1.20353

And now in Haskell, using the same mechanism we tried earlier:

> let xs = runif 3
> :t xs
xs :: IO [Double]
> sum xs
<interactive>:16:1:
    No instance for (Num [Double]) arising from a use of ‘sum’
    In the expression: sum xs
    In an equation for ‘it’: it = sum xs

This means that to deal with the numbers we generate, we have to treat them a little differently than we would in R, or compared to the situation where we were managing the RNG explicitly in Haskell. Concretely: if we use a monad to manage the RNG for us, then the numbers we generate will be ‘tagged’ by the monad. So we need to do something or other to make those tagged numbers work with ‘untagged’ numbers, or functions designed to work with ‘untagged’ numbers.

This is where things get confusing for beginners. Here’s how we could add up some random numbers in GHCi:

> xs <- runif 3
> sum xs
1.512024272587933

We’ve used the <- symbol to bind the result of runif 3 to the name xs, rather than let xs = .... But this is sort of particular to running code in GHCi; if you try to do this in a generic Haskell function, you’ll possibly wind up with some more weird type errors. To do this in regular ol’ Haskell code, you need to both use <--style binding and also acknowledge the ‘tagged’ nature of randomly-generated values.

The crux is that, when you’re using a monad to generate random numbers in Haskell, you need to separate generating them from using them. Rather than try to explain what I mean here precisely, let’s rely on example, and implement a simple Metropolis sampler for illustration.

A Metropolis Sampler

The Metropolis algorithm will help you approximate expectations over certain probability spaces. Here’s how it works. Picture yourself strolling around some bumpy landscape; you want to walk around it in such a fashion that you visit regions of it with probability proportional to their altitude. To do that, you can repeatedly:

Pick a random point near your current location.
Compare your present altitude to the altitude of that point you picked. Calculate a probability based on their ratio.
Flip a coin where the chance of observing a head is equal to that probability. If you get a head, move to the location you picked. Otherwise, stay put.

Let’s implement it in Haskell, using a monadic random number generator to do so. This time we’re going to use mwc-random - a more industrial-strength randomness library that you can confidently use in production code.

mwc-random uses Marsaglia’s multiply-with-carry algorithm to generate pseudo-random numbers. It requires you to explicitly create and pass a RNG to functions that need to generate random numbers, but it uses a monad to update the RNG state itself. This winds up being pretty nice; let’s dive in to see.

Create a module called Metropolis.hs and get some imports out of the way:

module Metropolis where

import Control.Monad
import Control.Monad.Primitive
import System.Random.MWC as MWC
import System.Random.MWC.Distributions as MWC

Step One

The first thing we want to do is implement is point (1) from above:

Pick a random point near your current location.

We’ll just use a standard normal distribution of the appropriate dimension to do this - we just want to take a location, perturb it, and return the perturbed location.

propose :: [Double] -> Gen RealWorld -> IO [Double]
propose location rng = traverse (perturb rng) location where
  perturb gen x = MWC.normal x 1 gen

So at finer detail: we’re walking over the coordinates of the current location and generating a normally-distributed value centered at each coordinate. The MWC.normal function will do this for a given mean and standard deviation, and we can use the traverse function to walk over each coordinate.

Note that we pass a mwc-random RNG - the value with type Gen RealWorld - to the propose function. We need to supply this generator anywhere we want to generate random numbers, but we don’t need to manually worry about tracking and updating its state. The IO monad will do that for us. The resulting randomly-generated values will be tagged with IO, so we’ll need to deal with that appropriately.

Step Two

Now let’s implement point (2):

Compare your present altitude to the altitude of that point you picked. Calculate a probability based on their ratio.

So, we need a function that will compare the altitude of our current point to the altitude of a proposed point and compute a probability from that. The following will do: it takes a function that will compute a (log-scale) altitude for us, as well as the current and proposed locations, and returns a probability.

moveProbability :: ([Double] -> Double) -> [Double] -> [Double] -> Double
moveProbability altitude current proposed =
    whenNaN 0 (exp (min 0 (altitude proposed - altitude current)))
  where
    whenNaN val x
      | isNaN x   = val
      | otherwise = x

Step Three

Finally, the third step of the algorithm:

Flip a coin where the chance of observing a head is equal to that probability. If you get a head, move to the location you picked. Otherwise stay put.

So let’s get to it:

decide :: [Double] -> [Double] -> Double -> Gen RealWorld -> IO [Double]
decide current proposed prob rng = do
  accept <- MWC.bernoulli prob rng
  return $
    if   accept
    then proposed
    else current

Here we need to flip a coin, so we require a source of randomness again. The decide function thus takes another generator of type Gen RealWorld that we then supply to the MWC.bernoulli function, and the result - the final location - is once again wrapped in IO.

This function clearly demonstrates the typical way that you’ll deal with random numbers in Haskell code. decide is a monadic function, so it proceeds using do-notation. When you need to generate a random value - here we generate a random True or False value according to a Bernoulli distribution - you bind the result to a name using the <- symbol. Then afterwards, in the scope of the function, you can use the bound value as if it were pure. But the entire function must still return a ‘wrapped-up’ value that makes the effect of passing the generator explicit at the type level; right here, that means that the value will be wrapped up in IO.

Putting Everything Together

The final Metropolis transition is a combination of steps one through three. We can put them together like so:

metropolis :: ([Double] -> Double) -> [Double] -> Gen RealWorld -> IO [Double]
metropolis altitude current rng = do
  proposed <- propose current rng
  let prob = moveProbability altitude current proposed
  decide current proposed prob rng

Again, metropolis is monadic, so we start off with a do to make monadic programming easy on us. Whenever we need a random value, we bind the result of a random number-returning function using the <- notation.

The propose function returns a random location, so we bind its result to the name proposed using the <- symbol. The moveProbability function, on the other hand, is pure - so we bind that using a let prob = ... expression. The decide function returns a random value, so we can just plop it right on the end here. The entire result of the metropolis function is random, so it is wrapped up in IO.

The result of metropolis is just a single transition of the Metropolis algorithm, which involves doing this kind of thing over and over. If we do that, we observe a bunch of points that trace out a particular realization of a Markov chain, which we can generate as follows:

chain
  :: Int -> ([Double] -> Double) -> [Double] -> Gen RealWorld -> IO [[Double]]
chain epochs altitude origin rng = loop epochs [origin] where
  loop n history@(current:_)
    | n <= 0    = return history
    | otherwise = do
        next <- metropolis altitude current rng
        loop (n - 1) (next:history)

An Example

Now that we have our chain function, we can use it to trace out a collection of points visited on a realization of a Markov chain. Remember that we’re supposed to be wandering over some particular abstract landscape; here, let’s stroll over the one defined by the following function:

landscape :: [Double] -> Double
landscape [x0, x1] =
  -0.5 * (x0 ^ 2 * x1 ^ 2 + x0 ^ 2 + x1 ^ 2 - 8 * x0 - 8 * x1)

What we’ll now do is pick an origin to start from, wander over the landscape for some number of steps, and then print the resulting realization of the Markov chain to stdout. We’ll do all that through the following main function:

main :: IO ()
main = do
  rng <- MWC.createSystemRandom
  let origin = [-0.2, 0.3]
  trace <- chain 1000 landscape origin rng
  mapM_ print trace

Running that will dump a trace to stdout. If you clean it up and plot it, you’ll see that the visited points have traced out a rough approximation of the landscape:

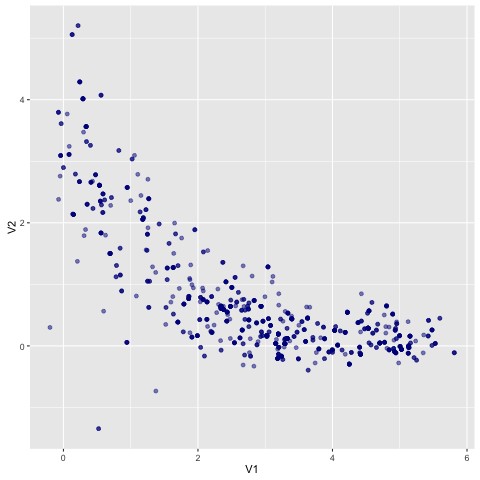
Fini

Hopefully this gives a broad idea of how to go about using random numbers in Haskell. I’ve talked about:

Why randomness in Haskell isn’t as simple as randomness in (say) Python or R.
How to handle randomness in Haskell, either by manual generator management or by offloading that job to a monad.
How to get thing done when a monad manages the generator for you - separating random number generation from random number processing.
Doing all the above with an industrial-strength RNG, using a simple Metropolis algorithm as an example.

Hopefully the example gives you an idea of how to work with random numbers in practice.

I’ll be the first to admit that randomness in Haskell requires more work than randomness in a language like R, which to this day remains my go-to interactive data analysis language of choice. Using randomness effectively in Haskell requires a decent understanding of how to work with monadic code, even if one doesn’t quite understand monads entirely yet.

What I can say is that when one has developed some intuition for monads - acquiring a ‘feel’ for how to work with monadic functions and values - the difficulty and awkwardness drop off a bit, and working with randomness feels no different than working with any other effect.

Happy generating! I’ve dumped the code for the Metropolis example into a gist.

For a more production-quality Metropolis sampler, you can check out my mighty-metropolis library, which is a member of the declarative suite of MCMC algos.

jtobin.io