Revenge of the Builders

I wanted to make a quick addendum to my last post in that I did some further experimenting with Data.ByteString.Builder on both the base16 encoding and decoding tasks, comparing results with the impure direct-allocation-and-write-based implementations I mentioned previously.

I had remarked that builders can be pretty efficient if you’re careful to pack your data aggressively, such that you don’t wind up needing to use too many builders in the first place. I decided to try minimising, as in objectively minimising, the number of builders required in both base16 encoding & decoding, to see what kind of performance I could squeeze out while sticking to the pure API. The builders didn’t disappoint.

How would one “objectively minimise” the number of builders required here? Simply by processing the biggest-sized chunk possible at a time, given we always want to write a Word64. If we can’t do that, we’ll write a Word32 and a Word16 and a Word8. If we can’t do that, we’ll write a Word32 and a Word16. And so on. We can figure all this out just by doing some checks on the length of the input bytestring when starting out: we trade some additional cheap arithmetic operations on machine integers up-front for fewer expensive builder allocations further down the line.

For encoding, this means doing the following checks:

encode :: BS.ByteString -> BS.ByteString
encode bs@(BI.PS _ _ l)
    | l < 64    = to_strict_small loop
    | otherwise = to_strict loop
  where
    loop
      | l `rem` 4 == 0 = go64 bs
      | (l - 3) `rem` 4 == 0 = case BS.splitAt (l - 3) bs of
          (chunk, etc) ->
               go64 chunk
            <> go32 (BU.unsafeTake 2 etc)
            <> go16 (BU.unsafeDrop 2 etc)
      | (l - 2) `rem` 4 == 0 = case BS.splitAt (l - 2) bs of
          (chunk, etc) -> go64 chunk <> go32 etc
      | (l - 1) `rem` 4 == 0 = case BS.splitAt (l - 1) bs of
          (chunk, etc) -> go64 chunk <> go16 etc

      | l `rem` 2 == 0 = go32 bs
      | (l - 1) `rem` 2 == 0 = case BS.splitAt (l - 1) bs of
          (chunk, etc) -> go32 chunk <> go16 etc

      | otherwise = go16 bs

where each ‘go’ function writes words with the indicated number of bits at a time, e.g.:

go64 b = case BS.splitAt 4 b of
  (chunk, etc)
    | BS.null chunk -> mempty
    | otherwise ->
        let !w16_0 = expand_w8 (BU.unsafeIndex chunk 0)
            !w16_1 = expand_w8 (BU.unsafeIndex chunk 1)
            !w16_2 = expand_w8 (BU.unsafeIndex chunk 2)
            !w16_3 = expand_w8 (BU.unsafeIndex chunk 3)

            !w64 = fi w16_0 `B.shiftL` 48
               .|. fi w16_1 `B.shiftL` 32
               .|. fi w16_2 `B.shiftL` 16
               .|. fi w16_3

        in  BSB.word64BE w64 <> go64 etc

and where expand_w8 is just a variant of the previous ‘hilo’ function that returns a Word16 directly, rather than a pair of Word8’s.

‘go32’ works on a chunk of size two, writing a single Word32, and ‘go16’ on a chunk of size one, writing a Word16. The point of having all these functions is that we can now always write the largest-sized word that we can, instead of writing Word8’s or Word16’s exclusively.

(Decoding works similarly, except we need more checks, and an additional ‘go8’ function to handle the one-byte case. I won’t paste the salad of conditionals required here.)

In any case, by employing this strategy we can come pretty close to the performance of the impure implementations. Here are some benchmark results for encoding a 1kb input:

benchmarking encode/ppad-base16
time                 5.929 μs   (5.847 μs .. 6.013 μs)
                     0.999 R²   (0.998 R² .. 0.999 R²)
mean                 5.975 μs   (5.913 μs .. 6.057 μs)
std dev              233.1 ns   (172.4 ns .. 310.0 ns)

benchmarking encode/base16-bytestring
time                 3.246 μs   (3.233 μs .. 3.262 μs)
                     1.000 R²   (1.000 R² .. 1.000 R²)
mean                 3.284 μs   (3.268 μs .. 3.303 μs)
std dev              61.05 ns   (47.83 ns .. 76.77 ns)

benchmarking encode/base16
time                 3.236 μs   (3.221 μs .. 3.253 μs)
                     1.000 R²   (1.000 R² .. 1.000 R²)
mean                 3.244 μs   (3.233 μs .. 3.256 μs)
std dev              37.31 ns   (31.87 ns .. 47.21 ns)

Case                        Allocated  GCs
ppad-base16 (encode)           53,704    0
base16-bytestring (encode)      2,272    0
base16 (encode)                 2,256    0

We’re allocating 25x more than the impure versions, but are only 2x slower or less. Here’s the decoding story:

benchmarking decode/ppad-base16
time                 4.942 μs   (4.884 μs .. 4.995 μs)
                     0.999 R²   (0.998 R² .. 0.999 R²)
mean                 4.908 μs   (4.854 μs .. 4.964 μs)
std dev              176.8 ns   (150.3 ns .. 214.3 ns)
variance introduced by outliers: 46% (moderately inflated)

benchmarking decode/base16-bytestring
time                 540.8 ns   (533.7 ns .. 548.2 ns)
                     0.999 R²   (0.999 R² .. 0.999 R²)
mean                 541.6 ns   (536.9 ns .. 547.5 ns)
std dev              17.64 ns   (13.87 ns .. 22.24 ns)
variance introduced by outliers: 47% (moderately inflated)

benchmarking decode/base16
time                 555.8 ns   (549.7 ns .. 560.9 ns)
                     0.999 R²   (0.999 R² .. 1.000 R²)
mean                 550.7 ns   (546.7 ns .. 555.5 ns)
std dev              15.46 ns   (13.11 ns .. 18.97 ns)
variance introduced by outliers: 39% (moderately inflated)

Case                        Allocated  GCs
ppad-base16 (decode)           21,960    0
base16-bytestring (decode)        128    0
base16 (decode)                 2,440    0

We’re allocating less (we’re writing less), but are closer to 10x slower. Not too bad, all things considered!

(N.b., it’s worth noting that the impure decoding functions also use what appears to be a more efficient lookup table to convert from hex characters back to Word8, so that may account for some of the differential there.)

Fast Haskell, Redux

In this post I’m going to incrementally optimise a simple base16 (hexadecimal) encoding routine and illustrate what sort of performance boost each optimisation yields. Hopefully it can be used to glean a bit about what tends to make Haskell code fast – especially code that deals with bytestrings.

You can think of this as a kind of supplement to Chris Done’s Fast Haskell: Competing with C at parsing XML post from a few years ago. Here, like in Chris’s example, we’re going to focus a lot on bytestring handling, though we’ll deal with some different issues than he faced, and also eventually go a little lower-level on the bytestring side of things.

Base16 Encoding

Let’s get right into it. The basic idea here is: for each byte (Word8) in an input, extract its high and low bits, and then map each (effectively a Word4) to a character from the hex alphabet:

import qualified Data.Bits as B
import qualified Data.ByteString as BS

hex_charset :: BS.ByteString
hex_charset = "0123456789abcdef"

hilo :: Word8 -> (Word8, Word8)
hilo b =
  let hi = BS.index hex_charset (fromIntegral b `B.shiftR` 4)
      lo = BS.index hex_charset (fromIntegral b .&. 0b00001111)
  in  (hi, lo)

You then get a base16-encoded output by gluing the resulting characters together in the appropriate fashion:

encode :: BS.ByteString -> BS.ByteString
encode bs = go mempty 0
  where
    l = BS.length bs
    go !acc j
      | j == l = BS.reverse acc
      | otherwise =
          let (hi, lo) = hilo (BS.index bs j)
          in  go (BS.cons lo (BS.cons hi acc)) (succ j)

There are some things here that might stick out to someone accustomed to writing performant Haskell code, but it’s an otherwise reasonable-looking first take. How does it perform on a 1kb input?

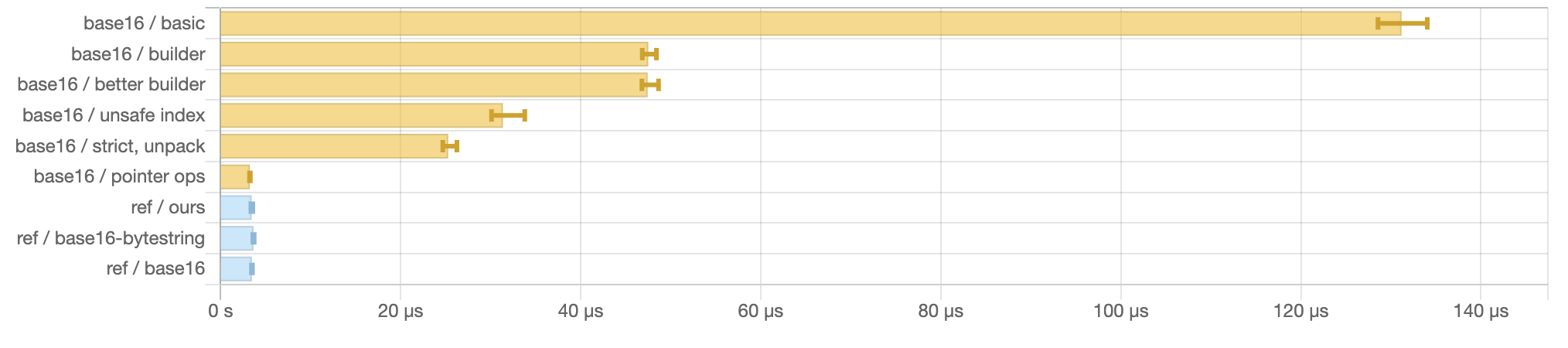
benchmarking base16/basic
time                 114.2 μs   (113.1 μs .. 115.4 μs)
                     0.999 R²   (0.998 R² .. 1.000 R²)
mean                 116.1 μs   (115.1 μs .. 118.3 μs)
std dev              4.453 μs   (2.609 μs .. 8.263 μs)
variance introduced by outliers: 38% (moderately inflated)

                 Allocated  GCs
basic            2,326,160    0

Well, according to weigh it seems to allocate a ton. The primary issue is that every invocation of the ‘cons’ function creates a copy of its input bytestring; this is the main thing that would scream out at an experienced Haskeller if they were to glance at the above code. We’re not dealing with O(1) ‘cons’ in bytestring-land, as we are when we use lists.

(As a side note: although ‘BS.reverse’ might raise an eyebrow, it’s actually really fast. It’s a FFI call to a C reverse routine.)

Builders

A more efficient way to construct bytestrings is via Data.ByteString.Builder, which supports constant-time concatenation of sequences of bytes. Here’s a version of ‘encode’ that uses builders:

import qualified Data.ByteString.Builder as BSB

to_strict :: BSB.Builder -> BS.ByteString
to_strict = BS.toStrict . BSB.toLazyByteString
{-# INLINE to_strict #-}

encode :: BS.ByteString -> BS.ByteString
encode bs = to_strict (go 0)
  where
    l = BS.length bs
    go j
      | j == l = mempty
      | otherwise =
          let (hi, lo) = hilo (BS.index bs j)
          in  BSB.word8 hi <> BSB.word8 lo <> go (succ j)

There’s a new function to convert the builder back to a strict bytestring, and now we concatenate builder singletons in order. Simple enough. How does it compare in terms of performance?

benchmarking base16/builder
time                 42.54 μs   (42.01 μs .. 43.27 μs)
                     0.999 R²   (0.999 R² .. 0.999 R²)
mean                 42.88 μs   (42.57 μs .. 43.22 μs)
std dev              1.105 μs   (946.6 ns .. 1.387 μs)
variance introduced by outliers: 24% (moderately inflated)

                 Allocated  GCs
builder            397,768    0

Much better. It allocates about 6x less and is almost 3x faster.

Builders are definitely worth knowing about when dealing with bytestrings, as they’re easy to use, and allow one to write pure code that performs reasonably well. There’s also some fine-tining you can do in order to squeeze additional performance out of them in certain cases. For small inputs, you can use a custom strategy to more efficiently convert builders to lazy bytestrings en route to a strict one, e.g.:

import qualified Data.ByteString.Builder.Extra as BE

to_strict_small :: BSB.Builder -> BS.ByteString
to_strict_small = BS.toStrict
  . BE.toLazyByteStringWith (BE.safeStrategy 128 BE.smallChunkSize) mempty

Using less builders helps as well, and probably even moreso. Consider the following, in which the loop writes a single Word16 at a time instead of two Word8’s:

encode :: BS.ByteString -> BS.ByteString
encode bs@(BI.PS _ _ l)
    | l < 128 = to_strict_small (go 0)
    | otherwise = to_strict (go 0)
  where
    go j
      | j == l = mempty
      | otherwise =
          let (hi, lo) = hilo (BS.index bs j)
              w16 = fromIntegral hi `B.shiftL` 8
                .|. fromIntegral lo
          in  BSB.word16BE w16 <> go (succ j)

It allocates slightly less, and is a microsecond peppier, because there’s just less building going on:

benchmarking base16/better builder
time                 40.96 μs   (40.64 μs .. 41.33 μs)
                     0.999 R²   (0.999 R² .. 1.000 R²)
mean                 41.12 μs   (40.79 μs .. 41.48 μs)
std dev              1.163 μs   (969.0 ns .. 1.494 μs)
variance introduced by outliers: 28% (moderately inflated)

                 Allocated  GCs
better builder     389,592    0

(Note that I’ve also introduced the use of the ‘BI.PS’ pattern synonym here, but only to more easily grab the input bytestring’s length. It has nothing to do with performance.)

Unsafe Functions

Another easy gain can be won by replacing the calls to bytestring’s ‘index’ with its ‘unsafeIndex’ variant:

import qualified Data.ByteString.Unsafe as BU

hilo :: Word8 -> (Word8, Word8)
hilo b =
  let hi = BU.unsafeIndex hex_charset (fromIntegral b `B.shiftR` 4)
      lo = BU.unsafeIndex hex_charset (fromIntegral b .&. 0b00001111)
  in  (hi, lo)

encode :: BS.ByteString -> BS.ByteString
encode bs@(BI.PS _ _ l)
    | l < 128 = to_strict_small (go 0)
    | otherwise = to_strict (go 0)
  where
    go j
      | j == l = mempty
      | otherwise =
          let (hi, lo) = hilo (BU.unsafeIndex bs j)
              w16 = fromIntegral hi `B.shiftL` 8
                .|. fromIntegral lo
          in  BSB.word16BE w16 <> go (succ j)

It often makes sense to do this so long as you can prove that the call is actually safe (the compiler, of course, can’t), as ‘unsafeIndex’ reliably yields a decent performance boost. In this case, the unsafe indexing into the hex alphabet in ‘hilo’ is being done with what are effectively four-bit words, which will always be safe to use as indices in a 16-length bytestring (there are 2^4 = 16 distinct Word4’s). The unsafe index called in the body of the loop can similarly be verified to remain safely within the input bytestring’s bounds, since the loop terminates when its index argument hits the end.

The performance now:

benchmarking base16/unsafe index
time                 25.58 μs   (25.25 μs .. 25.89 μs)
                     0.998 R²   (0.997 R² .. 0.999 R²)
mean                 25.69 μs   (25.41 μs .. 26.03 μs)
std dev              1.051 μs   (852.3 ns .. 1.396 μs)
variance introduced by outliers: 47% (moderately inflated)

                 Allocated  GCs
unsafe index       233,944    0

Another substantial win. Much less allocation and a great reduction in wall-clock time.

Note however that not all unsafe functions will yield a boost as impressive as bytestring’s ‘unsafeIndex’. I’ve never found the ‘unsafeShiftL’ and ‘unsafeShiftR’ functions in Data.Bits to ever really seem to do much at all, for example, so we’ll keep the plain ‘B.shiftR’ call in ‘hilo’ above.

Unboxed Primitives

Next up is another optimisation that any seasoned Haskeller should know about: use unboxed types, unless there’s some unusual reason not to.

Unboxed values require no allocation. To quote the GHC user guide:

The representation of a Haskell Int, for example, is a two-word heap object. An unboxed type, however, is represented by the value itself, no pointers or heap allocation are involved.

Unboxed types correspond to the “raw machine” types you would use in C: Int# (long int), Double# (double), Addr# (void *), etc. The primitive operations (PrimOps) on these types are what you might expect; e.g., (+#) is addition on Int#s, and is the machine-addition that we all know and love—usually one instruction.

You can work with unboxed types and values explicitly by using the appropriate imports and the MagicHash pragma, which can actually be pretty nice, because you express what’s really going on, but more commonly, unboxed types are denoted via strictness annotations and the UNPACK pragma, like so:

data W8Pair = Pair
  {-# UNPACK #-} !Word8
  {-# UNPACK #-} !Word8

hilo :: Word8 -> W8Pair
hilo b =
  let !hi = BU.unsafeIndex hex_charset (fromIntegral b `B.shiftR` 4)
      !lo = BU.unsafeIndex hex_charset (fromIntegral b .&. 0b00001111)
  in  Pair hi lo

encode :: BS.ByteString -> BS.ByteString
encode bs@(BI.PS _ _ l)
    | l < 128 = to_strict_small (go 0)
    | otherwise = to_strict (go 0)
  where
    go j
      | j == l = mempty
      | otherwise =
          let !(Pair hi lo) = hilo (BU.unsafeIndex bs j)
          in  BSB.word8 hi <> BSB.word8 lo <> go (succ j)

Now ‘hilo’ as a whole – so long as one compiles with optimisation – simply doesn’t allocate at all, and the overall allocation and wall-clock time are trimmed by a decent chunk yet again:

benchmarking base16/strict, unpack
time                 20.90 μs   (20.56 μs .. 21.25 μs)
                     0.998 R²   (0.998 R² .. 0.999 R²)
mean                 20.97 μs   (20.76 μs .. 21.19 μs)
std dev              742.1 ns   (619.9 ns .. 938.1 ns)
variance introduced by outliers: 41% (moderately inflated)

                 Allocated  GCs
strict, unpack     176,600    0

At this point the allocation is absolutely dominated by the builders, so if we want to do better we’ll need to do something about them.

Direct Allocation and Writes

A strict ByteString is just a wrapper around some memory. It’s defined in recent versions via:

data ByteString = BS
  {-# UNPACK #-} !(ForeignPtr Word8) -- payload
  {-# UNPACK #-} !Int                -- length

So, a “foreign pointer” to some memory location and a length (where a foreign pointer means a pointer to something that isn’t managed by the RTS in the same way normal data is). To most efficiently create a bytestring, one can thus do it in the same way one would do so in C: allocate some memory and write to it directly.

This is the line beyond which one probably can’t consider his code to be “pure Haskell” anymore. An ‘unsafePerformIO’ call or similar isn’t technically going to be required (it could be masked via ‘Data.ByteString.Internal.unsafeCreate’, for example), and one still doesn’t need to type the {-# LANGUAGE FFI #-} pragma at the top of his module. But it’s safe to say that any assertions of purity would at this point be at least somewhat controversial.

But if one does want to wield this particular Ring of Power, it can be done like so (this is basically what Bryan O’Sullivan’s base16-bytestring or Emily Pillmore’s base16 package do, for example):

import Foreign.Ptr
import Foreign.Storable
import GHC.ForeignPtr
import GHC.Word
import System.IO.Unsafe

encode :: BS.ByteString -> BS.ByteString
encode (BI.PS bs _ l) = unsafeDupablePerformIO $ do
    buffer <- mallocPlainForeignPtrBytes (l * 2)

    withForeignPtr buffer $ \p_buf ->
      withForeignPtr bs $ \p_src ->
        go p_buf p_src (p_src `plusPtr` l)

    pure (BI.BS buffer (l * 2))
  where
    go !buf !src !end
      | src == end = pure ()
      | otherwise = do
          !b <- peek src
          let !(Pair hi lo) = hilo b
          poke buf hi
          poke (buf `plusPtr` 1) lo
          go (buf `plusPtr` 2) (src `plusPtr` 1) end

Here we allocate a buffer explicitly and loop through the input bytestring’s allocated memory, rather than its Haskell representation, in order to populate it, wrapping the result up in a new bytestring via the raw ‘BI.BS’ constructor. It’s worth noting that we could still just make use of ‘unsafeIndex’ on the input bytestring if we wanted, rather than making direct use of its foreign pointer, but since we’re already going big, why not go all the way?

This function allocates minimally, and indeed is at parity with the relevant “encode” functions found in both the base16 and base16-bytestring packages in terms of wall-clock time. It’s about 50x faster than the initial naïve version, and perhaps 5x faster than the most efficient version that used builders:

benchmarking base16/pointer ops
time                 2.929 μs   (2.903 μs .. 2.959 μs)
                     1.000 R²   (0.999 R² .. 1.000 R²)
mean                 2.950 μs   (2.936 μs .. 2.967 μs)
std dev              52.87 ns   (43.32 ns .. 64.89 ns)
variance introduced by outliers: 18% (moderately inflated)

                 Allocated  GCs
pointer ops            120    0

I’m guessing this is probably about as fast as one can make this function via “normal” means. Other techniques that I tried while preparing this article don’t seem to move the needle much on this problem, if at all. I’d be pretty impressed by anything that produced another order-of-magnitude performance boost, though – if anyone can achieve that, I’d love to hear about it!

Recap

So to conclude with a quick, advice-laden summary of the techniques used here:

• Avoid using BS.cons, BS.append, and so on, as each requires making a copy of their input bytestring or bytestrings. Instead, prefer builders, and try to pack your data so that you can get away with as few of them as possible. If you can write an occasional Word64, that’s much better than writing many Word8’s.

  It’s worth nothing, though, that occasional uses of cons, append, etc. on small inputs can be very benign, and even hard to beat by clever rewriting. You don’t always need to reach for builders or harder-core optimisations every time you want to glue a few bytestrings together. Consider this HMAC implementation from ppad-sha256:

  hmac
    :: BS.ByteString
    -> BS.ByteString
    -> BS.ByteString
  hmac mk@(BI.PS _ _ l) text =
      let step1 = k <> BS.replicate (64 - lk) 0x00
          step2 = BS.map (B.xor 0x36) step1
          step3 = step2 <> text
          step4 = hash step3
          step5 = BS.map (B.xor 0x5C) step1
          step6 = step5 <> step4
      in  hash step6
    where
      !(KeyAndLen k lk)
        | l > 64    = KeyAndLen (hash mk) 32
        | otherwise = KeyAndLen mk l
  

  It looks like there’s a lot of unnecessary copying going on here, but in the grand scheme of things, it’s simply not that much, and the bytestring functions are highly optimised, after all. I wasn’t able to improve this function’s performance either by builders or even low-level allocations and writes, including manually minimising allocations, reusing memory areas, and so on. The story would be different if I were calling these functions many times in a loop, though, at which point builders or direct writes would definitely prove useful.

• Don’t necessarily shy away from unsafe functions if said use can be proven to be perfectly safe. Aside from ‘unsafeIndex’, other things can be useful, particularly ‘unsafeTake’ and ‘unsafeDrop’. These can provide great performance boosts, though if one is not gunning for absolute, maximum performance, then sure, it might be better to avoid them.

  It’s also worth nothing that there are some useful unsafe functions that don’t exist in the bytestring API, but that can be assembled manually. Take this home-cooked unsafe splitAt, for example, that does no bounds checking:

  data SSPair = SSPair
    {-# UNPACK #-} !BS.ByteString
    {-# UNPACK #-} !BS.ByteString
  
  unsafe_splitAt :: Int -> BS.ByteString -> SSPair
  unsafe_splitAt n (BI.BS x l) =
    SSPair (BI.BS x n) (BI.BS (plusForeignPtr x n) (l - n))
  

• Make data strict unless you for some reason need it to be lazy, and always unpack strict fields when it’s possible to do so. You can also use -funbox-strict-fields or -funbox-small-strict-fields to unbox all strict fields at the module level, though I generally prefer the more explicit local use of UNPACK pragmas.

• Don’t be afraid to use low-level allocation and writes where it makes sense to do so. It may be unnecessary, even in highly-optimised library code (I chose to use builders in ppad-bech32 because we’re never dealing with large outputs there, for example), but it’s a great technique to have around for when performance really counts.

If you’d like to play with the code yourself, I’ve pushed it to this GitHub repo. Presuming you have flake support enabled, you can use ‘nix develop’ to enter a Nix shell, and then e.g. ‘cabal repl’ to open GHCi, or ‘cabal bench’ to run the benchmark suite. Enjoy!

Retvrning to X

I nuked all of my social media accounts years ago and never looked back. My general take is that all legacy web 2.0-style social media stuff needs to be ground under a boot, and then the boot filled with cement and sank to the bottom of a particularly deep ocean. Just in case.

That said, I recently recreated an account on X using my old handle, @jaredtobin (some other dude has nabbed @jtobin, unfortunately), and will be experimenting with it for traditional microblogging purposes for things that don’t warrant a full post on this, my trusty long-form blog.

Why not nostr, etc.? Well, I could. I like nostr, and maybe I’ll mirror my stuff there just for the lulz. But, pragmatically, X appears to be where the action is, and I want my stuff to be easy to access and interact with.

It’s an experiment. I’m aloof by nature, so there’s no guarantee I won’t at some point turn up my nose and redeploy the nukes. But we’ll see how it goes. Follow me there, if you’re into that kind of thing!