Monadic Recursion Schemes

I have another few posts that I’d like to write before cluing up the whole recursion schemes kick I’ve been on. The first is a simple note about monadic versions of the schemes introduced thus far.

In practice you often want to deal with effectful versions of something like cata. Take a very simple embedded language, for example (“Hutton’s Razor”, with variables):

{-# LANGUAGE DeriveFunctor #-}
{-# LANGUAGE DeriveFoldable #-}
{-# LANGUAGE DeriveTraversable #-}
{-# LANGUAGE LambdaCase #-}

import           Control.Monad              ((<=<), liftM2)
import           Control.Monad.Trans.Class  (lift)
import           Control.Monad.Trans.Reader (ReaderT, ask, runReaderT)
import           Data.Functor.Foldable      hiding (Foldable, Unfoldable)
import qualified Data.Functor.Foldable      as RS (Foldable, Unfoldable)
import           Data.Map.Strict            (Map)
import qualified Data.Map.Strict            as Map

data ExprF r =
    VarF String
  | LitF Int
  | AddF r r
  deriving (Show, Functor, Foldable, Traversable)

type Expr = Fix ExprF

var :: String -> Expr
var = Fix . VarF

lit :: Int -> Expr
lit = Fix . LitF

add :: Expr -> Expr -> Expr
add a b = Fix (AddF a b)

(Note: Make sure you import ‘Data.Functor.Foldable.Foldable’ with a qualifier because GHC’s ‘DeriveFoldable’ pragma will become confused if there are multiple ‘Foldables’ in scope.)

Take proper error handling over an expression of type ‘Expr’ as an example; at present we’d have to write an ‘eval’ function as something like

eval :: Expr -> Int
eval = cata $ \case
  LitF j   -> j
  AddF i j -> i + j
  VarF _   -> error "free variable in expression"

This is a bit of a non-starter in a serious or production implementation, where errors are typically handled using a higher-kinded type like ‘Maybe’ or ‘Either’ instead of by just blowing up the program on the spot. If we hit an unbound variable during evaluation, we’d be better suited to return an error value that can be dealt with in a more appropriate place.

Look at the algebra used in ‘eval’; what would be useful is something like

monadicAlgebra = \case
  LitF j   -> return j
  AddF i j -> return (i + j)
  VarF v   -> Left (FreeVar v)

data Error =
    FreeVar String
  deriving Show

This won’t fly with cata as-is, and recursion-schemes doesn’t appear to include any support for monadic variants out of the box. But we can produce a monadic cata - as well as monadic versions of the other schemes I’ve talked about to date - without a lot of trouble.

To begin, I’ll stoop to a level I haven’t yet descended to and include a commutative diagram that defines a catamorphism:

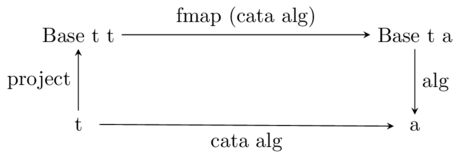
To read it, start in the bottom left corner and work your way to the bottom right. You can see that we can go from a value of type ‘t’ to one of type ‘a’ by either applying ‘cata alg’ directly, or by composing a bunch of other functions together.

If we’re trying to define cata, we’ll obviously want to do it in terms of the compositions:

cata:: (RS.Foldable t) => (Base t a -> a) -> t ->  a
cata alg = alg . fmap (cata alg) . project

Note that in practice it’s typically more efficient to write recursive functions using a non-recursive wrapper, like so:

cata:: (RS.Foldable t) => (Base t a -> a) -> t ->  a
cata alg = c where c = alg . fmap c . project

This ensures that the function can be inlined. Indeed, this is the version that recursion-schemes uses internally.

To get to a monadic version we need to support a monadic algebra - that is, a function with type ‘Base t a -> m a’ for appropriate ‘t’. To translate the commutative diagram, we need to replace ‘fmap’ with ‘traverse’ (requiring a ‘Traversable’ instance) and the final composition with monadic (or Kleisli) composition:

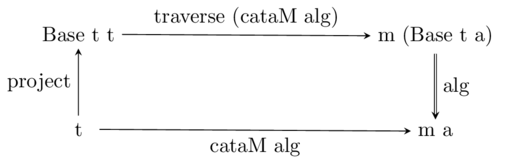
The resulting function can be read straight off the diagram, modulo additional constraints on type variables. I’ll go ahead and write it directly in the inline-friendly way:

cataM
  :: (Monad m, Traversable (Base t), RS.Foldable t)
  => (Base t a -> m a) -> t ->  m a
cataM alg = c where
  c = alg <=< traverse c . project

Going back to the previous example, we can now define a proper ‘eval’ as follows:

eval :: Expr -> Either Error Int
eval = cataM $ \case
  LitF j   -> return j
  AddF i j -> return (i + j)
  VarF v   -> Left (FreeVar v)

This will of course work for any monad. A common pattern on an ‘eval’ function is to additionally slap on a ‘ReaderT’ layer to supply an environment, for example:

eval :: Expr -> ReaderT (Map String Int) (Either Error) Int
eval = cataM $ \case
  LitF j   -> return j
  AddF i j -> return (i + j)
  VarF v   -> do
    env <- ask
    case Map.lookup v env of
      Nothing -> lift (Left (FreeVar v))
      Just j  -> return j

And just an example of how that works:

> let open = add (var "x") (var "y")
> runReaderT (eval open) (Map.singleton "x" 1)
Left (FreeVar "y")
> runReaderT (eval open) (Map.fromList [("x", 1), ("y", 5)])
Right 6

You can follow the same formula to create the other monadic recursion schemes. Here’s monadic ana:

anaM
  :: (Monad m, Traversable (Base t), RS.Unfoldable t)
  => (a -> m (Base t a)) -> a -> m t
anaM coalg = a where
  a = (return . embed) <=< traverse a <=< coalg

and monadic para, apo, and hylo follow in much the same way:

paraM
  :: (Monad m, Traversable (Base t), RS.Foldable t)
  => (Base t (t, a) -> m a) -> t -> m a
paraM alg = p where
  p   = alg <=< traverse f . project
  f t = liftM2 (,) (return t) (p t)

apoM
  :: (Monad m, Traversable (Base t), RS.Unfoldable t)
  => (a -> m (Base t (Either t a))) -> a -> m t
apoM coalg = a where
  a = (return . embed) <=< traverse f <=< coalg
  f = either return a

hyloM
  :: (Monad m, Traversable t)
  => (t b -> m b) -> (a -> m (t a)) -> a -> m b
hyloM alg coalg = h
  where h = alg <=< traverse h <=< coalg

These are straightforward extensions from the basic schemes. A good exercise is to try putting together the commutative diagrams corresponding to each scheme yourself, and then use them to derive the monadic versions. That’s pretty fun to do for para and apo in particular.

If you’re using these monadic versions in your own project, you may want to drop them into a module like ‘Data.Functor.Foldable.Extended’ as recommended by my colleague Jasper Van der Jeugt. Additionally, there is an old issue floating around on the recursion-schemes repo that proposes adding them to the library itself. So maybe they’ll turn up in there eventually.

Sorting Slower with Style

I previously wrote about implementing merge sort using recursion schemes. By using a hylomorphism we could express the algorithm concisely and true to its high-level description.

Insertion sort can be implemented in a similar way - this time by putting one recursion scheme inside of another.

Read on for details.

Apomorphisms

These guys don’t seem to get a lot of love in the recursion scheme tutorial du jour, probably because they might be the first scheme you encounter that looks truly weird on first glance. But apo is really not bad at all - I’d go so far as to call apomorphisms straightforward and practical.

So: if you remember your elementary recursion schemes, you can say that apo is to ana as para is to cata. A paramorphism gives you access to a value of the original input type at every point of the recursion; an apomorphism lets you terminate using a value of the original input type at any point of the recursion.

This is pretty useful - often when traversing some structure you just want to bail out and return some value on the spot, rather than continuing on recursing needlessly.

A good introduction is the toy ‘mapHead’ function that maps some other function over the head of a list and leaves the rest of it unchanged. Let’s first rig up a hand-rolled list type to illustrate it on:

{-# LANGUAGE DeriveFunctor #-}
{-# LANGUAGE TypeFamilies #-}

import Data.Functor.Foldable

data ListF a r =
    ConsF a r
  | NilF
  deriving (Show, Functor)

type List a = Fix (ListF a)

fromList :: [a] -> List a
fromList = ana coalg . project where
  coalg Nil        = NilF
  coalg (Cons h t) = ConsF h t

(I’ll come back to the implementation of ‘fromList’ later, but for now you can see it’s implemented via an anamorphism.)

Example One

Here’s ‘mapHead’ for our hand-rolled list type, implemented via apo:

mapHead :: (a -> a) -> List a -> List a
mapHead f = apo coalg . project where
  coalg NilF        = NilF
  coalg (ConsF h t) = ConsF (f h) (Left t)

Before I talk you through it, here’s a trivial usage example:

> fromList [1..3]
Fix (ConsF 1 (Fix (ConsF 2 (Fix (ConsF 3 (Fix NilF))))))
> mapHead succ (fromList [1..3])
Fix (ConsF 2 (Fix (ConsF 2 (Fix (ConsF 3 (Fix NilF))))))

Now. Take a look at the coalgebra involved in writing ‘mapHead’. It has the type ‘a -> Base t (Either t a)’, which for our hand-rolled list case simplifies to ‘a -> ListF a (Either (List a) a)’.

Just as a reminder, you can check this in GHCi using the ‘:kind!’ command:

> :set -XRankNTypes
> :kind! forall a. a -> Base (List a) (Either (List a) a)
forall a. a -> Base (List a) (Either (List a) a) :: *
= a -> ListF a (Either (List a) a)

So, inside any base functor on the right hand side we’re going to be dealing with some ‘Either’ values. The ‘Left’ branch indicates that we’re going to terminate the recursion using whatever value we pass, whereas the ‘Right’ branch means we’ll continue recursing as per normal.

In the case of ‘mapHead’, the coalgebra is saying:

• deconstruct the list; if it has no elements just return an empty list
• if the list has at least one element, return the list constructed by prepending ‘f h’ to the existing tail.

Here the ‘Left’ branch is used to terminate the recursion and just return the existing tail on the spot.

Example Two

That was pretty easy, so let’s take it up a notch and implement list concatenation:

cat :: List a -> List a -> List a
cat l0 l1 = apo coalg (project l0) where
  coalg NilF = case project l1 of
    NilF      -> NilF
    ConsF h t -> ConsF h (Left t)

  coalg (ConsF x l) = case project l of
    NilF      -> ConsF x (Left l1)
    ConsF h t -> ConsF x (Right (ConsF h t))

This one is slightly more involved, but the principles are almost entirely the same. If both lists are empty we just return an empty list, and if the first list has at most one element we return the list constructed by jamming the second list onto it. The ‘Left’ branch again just terminates the recursion and stops everything there.

If both lists are nonempty? Then we actually do some work and recurse, which is what the ‘Right’ branch indicates.

So hopefully you can see there’s nothing too weird going on - the coalgebras are really simple once you get used to the Either constructors floating around in there.

Paramorphisms involve an algebra that gives you access to a value of the original input type in a pair - a product of two values. Since apomorphisms are their dual, it’s no surprise that you can give them a value of the original input type using ‘Either’ - a sum of two values.

Insertion Sort

So yeah, my favourite example of an apomorphism is for implementing the ‘inner loop’ of insertion sort, a famous worst-case \(O(n^2)\) comparison-based sort. Granted that insertion sort itself is a bit of a toy algorithm, but the pattern used to implement its internals is pretty interesting and more broadly applicable.

This animation found on Wikipedia illustrates how insertion sort works:

We’ll actually be doing this thing in reverse - starting from the right-hand side and scanning left - but here’s the inner loop that we’ll be concerned with: if we’re looking at two elements that are out of sorted order, slide the offending element to where it belongs by pushing it to the right until it hits either a bigger element or the end of the list.

As an example, picture the following list:

[3, 1, 1, 2, 4, 3, 5, 1, 6, 2, 1]

The first two elements are out of sorted order, so we want to slide the 3 rightwards along the list until it bumps up against a larger element - here that’s the 4.

The following function describes how to do that in general for our hand-rolled list type:

coalg NilF        = NilF
coalg (ConsF x l) = case project l of
  NilF          -> ConsF x (Left l)
  ConsF h t
    | x <= h    -> ConsF x (Left l)
    | otherwise -> ConsF h (Right (ConsF x t))

It says:

• deconstruct the list; if it has no elements just return an empty list
• if the list has only one element, or has at least two elements that are in sorted order, terminate with the original list by passing the tail of the list in the ‘Left’ branch
• if the list has at least two elements that are out of sorted order, swap them and recurse using the ‘Right’ branch

And with that in place, we can use an apomorphism to put it to work:

knockback :: Ord a => List a -> List a
knockback = apo coalg . project where
  coalg NilF        = NilF
  coalg (ConsF x l) = case project l of
    NilF          -> ConsF x (Left l)
    ConsF h t
      | x <= h    -> ConsF x (Left l)
      | otherwise -> ConsF h (Right (ConsF x t))

Check out how it works on our original list, slotting the leading 3 in front of the 4 as required. I’ll use a regular list here for readability:

> let test = [3, 1, 1, 2, 4, 3, 5, 1, 6, 2, 1]
> knockbackL test
[1, 1, 2, 3, 4, 3, 5, 1, 6, 2, 1]

Now to implement insertion sort we just want to do this repeatedly like in the animation above.

This isn’t something you’d likely notice at first glance, but check out the type of ‘knockback . embed’:

> :t knockback . embed
knockback . embed :: Ord a => ListF a (List a) -> List a

That’s an algebra in the ‘ListF a’ base functor, so we can drop it into cata:

insertionSort :: Ord a => List a -> List a
insertionSort = cata (knockback . embed)

And voila, we have our sort.

If it’s not clear how the thing works, you can visualize the whole process as working from the back of the list, knocking back unsorted elements and recursing towards the front like so:

[]
[1]
[2, 1] -> [1, 2]
[6, 1, 2] -> [1, 2, 6]
[1, 1, 2, 6]
[5, 1, 1, 2, 6] -> [1, 1, 2, 5, 6]
[3, 1, 1, 2, 5, 6] -> [1, 1, 2, 3, 5, 6]
[4, 1, 1, 2, 3, 5, 6] -> [1, 1, 2, 3, 4, 5, 6]
[2, 1, 1, 2, 3, 4, 5, 6] -> [1, 1, 2, 2, 3, 4, 5, 6]
[1, 1, 1, 2, 2, 3, 4, 5, 6]
[1, 1, 1, 1, 2, 2, 3, 4, 5, 6]
[3, 1, 1, 1, 1, 2, 2, 3, 4, 5, 6] -> [1, 1, 1, 1, 2, 2, 3, 3, 4, 5, 6]
[1, 1, 1, 1, 2, 2, 3, 3, 4, 5, 6]

Wrapping Up

And that’s it! If you’re unlucky you may be sorting asymptotically worse than if you had used mergesort. But at least you’re doing it with style.

The ‘mapHead’ and ‘cat’ examples come from the unreadable Vene and Uustalu paper that first described apomorphisms. The insertion sort example comes from Tim Williams’s excellent recursion schemes talk.

As always, I’ve dumped the code for this article into a gist.

Addendum: Using Regular Lists

You’ll note that the ‘fromList’ and ‘knockbackL’ functions above operate on regular Haskell lists. The short of it is that it’s easy to do this; recursion-schemes defines a data family called ‘Prim’ that basically endows lists with base functor constructors of their own. You just need to use ‘Nil’ in place of ‘[]’ and ‘Cons’ in place of ‘(:)’.

Here’s insertion sort implemented in the same way, but for regular lists:

knockbackL :: Ord a => [a] -> [a]
knockbackL = apo coalg . project where
  coalg Nil        = Nil
  coalg (Cons x l) = case project l of
    Nil           -> Cons x (Left l)
    Cons h t
      | x <= h    -> Cons x (Left l)
      | otherwise -> Cons h (Right (Cons x t))

insertionSortL :: Ord a => [a] -> [a]
insertionSortL = cata (knockbackL . embed)

Yo Dawg We Heard You Like Derivatives

I noticed this article by Tom Ellis today that provides an excellent ‘demystified’ introduction to automatic differentiation. His exposition is exceptionally clear and simple.

Hopefully not in the spirit of re-mystifying things too much, I wanted to demonstrate that this kind of forward-mode automatic differentiation can be implemented using a catamorphism, which cleans up the various let statements found in Tom’s version (at the expense of slightly more pattern matching).

Let me first duplicate his setup using the standard recursion scheme machinery:

{-# LANGUAGE DeriveFunctor #-}
{-# LANGUAGE LambdaCase #-}

import Data.Functor.Foldable

data ExprF r =
    VarF
  | ZeroF
  | OneF
  | NegateF r
  | SumF r r
  | ProductF r r
  | ExpF r
  deriving (Show, Functor)

type Expr = Fix ExprF

Since my expression type uses a fixed-point wrapper I’ll define my own embedded language terms to get around it:

var :: Expr
var = Fix VarF

zero :: Expr
zero = Fix ZeroF

one :: Expr
one = Fix OneF

neg :: Expr -> Expr
neg x = Fix (NegateF x)

add :: Expr -> Expr -> Expr
add a b = Fix (SumF a b)

prod :: Expr -> Expr -> Expr
prod a b = Fix (ProductF a b)

e :: Expr -> Expr
e x = Fix (ExpF x)

To implement a corresponding eval function we can use a catamorphism:

eval :: Double -> Expr -> Double
eval x = cata $ \case
  VarF         -> x
  ZeroF        -> 0
  OneF         -> 1
  NegateF a    -> negate a
  SumF a b     -> a + b
  ProductF a b -> a * b
  ExpF a       -> exp a

Very clear. We just match things mechanically.

Now, symbolic differentiation. If you refer to the original diff function you’ll notice that in cases like Product or Exp there are uses of both an original expression and also its derivative. This can be captured simply by a paramorphism:

diff :: Expr -> Expr
diff = para $ \case
  VarF                     -> one
  ZeroF                    -> zero
  OneF                     -> zero
  NegateF (_, x')          -> neg x'
  SumF (_, x') (_, y')     -> add x' y'
  ProductF (x, x') (y, y') -> add (prod x y') (prod x' y)
  ExpF (x, x')             -> prod (e x) x'

Here the primes indicate derivatives in the usual fashion, and the standard rules of differentiation are self-explanatory.

For automatic differentiation we just do sort of the same thing, except we’re also also going to lug around the evaluated function value itself at each point and evaluate to doubles instead of other expressions.

It’s worth noting here: why doubles? Because the expression type that we’ve defined has no notion of sharing, and thus the expressions will blow up à la diff (to see what I mean, try printing the analogue of diff bigExpression in GHCi). This could probably be mitigated by incorporating sharing into the embedded language in some way, but that’s a topic for another post.

Anyway, a catamorphism will do the trick:

ad :: Double -> Expr -> (Double, Double)
ad x = cata $ \case
  VarF                     -> (x, 1)
  ZeroF                    -> (0, 0)
  OneF                     -> (1, 0)
  NegateF (x, x')          -> (negate x, negate x')
  SumF (x, x') (y, y')     -> (x + y, x' + y')
  ProductF (x, x') (y, y') -> (x * y, x * y' + x' * y)
  ExpF (x, x')             -> (exp x, exp x * x')

Take a look at the pairs to the right of the pattern matches; the first element in each is just the corresponding term from eval, and the second is just the corresponding term from diff (made ‘Double’-friendly). The catamorphism gives us access to all the terms we need, and we can avoid a lot of work on the right-hand side by doing some more pattern matching on the left.

Some sanity checks to make sure that these functions match up with Tom’s:

*Main> map (snd . (`ad` testSmall)) [0.0009, 1.0, 1.0001]
[0.12254834896191881,1.0,1.0003000600100016]
*Main> map (snd . (`ad` testBig)) [0.00009, 1.0, 1.00001]
[3.2478565715996756e-6,1.0,1.0100754777229357]

UPDATE:

I had originally defined ad using a paramorphism but noticed that we can get by just fine with cata.