More Recursive Stochastic Processes

Some years ago I wrote about using recursion schemes to encode stochastic processes in an embedded probabilistic programming setting. The crux of it was that recursion schemes allow one to “factor out” the probabilistic phenomena from the recursive structure of the process; the probabilistic stuff typically sits in the so-called coalgebra of the recursion scheme, while the recursion scheme itself dictates the manner in which the process evolves.

While it’s arguable as to whether this stuff is useful from a strictly practical perspective (I would suggest “not”), I think the intuition one gleans from it can be somewhat worthwhile, and my curious brain finds itself wandering back to the topic from time to time.

I happened to take a look at this sort of framework again recently and discovered that I couldn’t easily seem to implement a Chinese Restaurant Process (CRP) – a stochastic process famous from the setting of nonparametric Bayesian models – via either of the “standard” patterns I used throughout my Recursive Stochastic Processes post. This indicated that the recursive structure of the CRP differs from the others I studied previously, at least in the manner I was attempting to encode it in my particular embedded language setting.

So let’s take a look to see what the initial problem was, how one can resolve it, and what insights we can take away from it all.

Framework

Here’s a simple and slightly more refined version of the embedded probabilistic programming framework I introduced in some of my older posts. I’ll elide incidental details, such as common imports and noisy code that might distract from the main points.

First, some unfamiliar imports and minimal core types:

import qualified Control.Monad.Trans.Free as TF
import qualified System.Random.MWC.Probability as MWC

data ModelF r =
    BernoulliF Double (Bool -> r)
  | UniformF (Double -> r)
  deriving Functor

type Model = Free ModelF

As a quick refresher, an expression of type ‘Model’ denotes a probability distribution over some carrier type, and terms that construct, manipulate, or interpret values of type ‘Model’ constitute those of a simple embedded probabilistic programming language.

Importantly, here we’re using a very minimal such language, consisting only of two primitives: the Bernoulli distribution (which is a probability distribution over a coin flip) and the uniform distribution over the interval [0, 1]. A trivial model that draws a probability of success from a uniform distribution, and then flips a coin conditional on that probability, would look like this, for example:

model :: Model Bool
model = Free (UniformF (\u ->
  Free (BernoulliF pure))

(We could create helper functions such that programs in this embedded language would be nicer to write, but that’s not the focus of this post.)

We can construct expressions that denote stochastic processes by using the normal salad of recursion schemes. Here’s how we can encode a geometric distribution, for example, in which one counts the number of coin flips required to observe a head:

geometric :: Double -> Model Int
geometric p = apo coalg 1 where
  coalg n = TF.Free (BernoulliF p (\accept ->
    if   accept
    then Left (pure n)
    else Right (n + 1)))

The coalgebra isolates the probabilistic phenomena (a Bernoulli draw, i.e. a coin flip), and the recursion scheme determines how the process evolves (halting if a Bernoulli proposal is accepted). The coalgebra is defined in terms of the so-called base or pattern functor of the free monad type, defined in ‘Control.Monad.Trans.Free’ (see Practical Recursion Schemes for a refresher on base functors if you’re rusty).

The result is an expression in our embedded language, of course, and is completely abstract. If we want to sample from the model it encodes, we can use an interpreter like the following:

prob :: Model a -> MWC.Prob IO a
prob = iterM $ \case
  BernoulliF p f -> MWC.bernoulli p >>= f
  UniformF f     -> MWC.uniform >>= f

where the ‘MWC’-prefixed functions are sampling functions from the mwc-probability library, and ‘iterM’ is the familiar monadic catamorphism-like recursion scheme over the free monad. This will produce a function that can be sampled with ‘MWC.sample’ when provided with a PRNG.

Here’s what some samples look like:

ghci> gen <- MWC.create
ghci> replicateM 10 (MWC.sample (prob (geometric 0.1)) gen)
[1,9,13,3,4,3,13,1,4,17]

Chinese Restaurant Process

The CRP is described technically as a stochastic process over “finite integer partitions,” and, more memorably, over configurations of a particular sort of indefinitely-large Chinese restaurant. One is to imagine customers entering the restaurant sequentially; the first sits at the first table available, and each additional customer is either seated at a new table with probability proportional to some dispersion parameter, or is seated at an occupied table with probability proportional to the number of other customers already sitting there.

If each customer is labelled by how many others were in the restaurant when they entered, the result is, for ‘n’ total customers, a random partition of the natural numbers up to ‘n’. A particular realisation of the process, following the arrival of 10 customers, might look like the following:

[[9,8,7,6,4,2,0], [1], [5,3]]

This is a restaurant configuration after 10 arrivals, where each element is a table populated by the labelled customers.

One of the rules of explaining the CRP is that you always have to include a visualization like this:

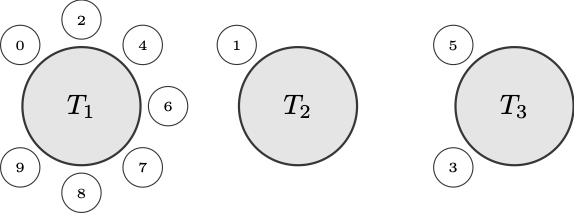
It corresponds to the realised sample, and we certainly wouldn’t want to break any pedagogical regulations.

Encoding, First Attempt

A natural way to encode the process is to seat each arriving customer at a new table with the appropriate probability, and then, if it turns out he is to be sat at an occupied table, to do that with the appropriate conditional probability (i.e., conditional on the fact that he’s not going to be seated at a new table).

So let’s imagine encoding a CRP with dispersion parameter ‘a’ and total number of customers ‘n’. Our first attempt might go something like this:

crp n a = ana coalg (1, <initial restaurant>) where
  coalg (customer, tables)
    | customer >= n = TF.Pure tables
    | otherwise =
        let p = <probability of seating customer at new table>
        in  TF.Free (BernoulliF p (\accept ->
              if   accept
              then (succ customer, <seat at new table>)
              else ???
            ))

We run into a problem when we hit the ‘else’ branch of the conditional. Here we want to express another random choice – viz., at which occupied table do we seat the arriving customer. We’d want to do something like ‘TF.Free (UniformF (\u -> …))’ in that ‘else’ branch and then use the produced uniform value to choose between the occupied tables based on their conditional probabilities. But that will prove to be impossible, given the type requirements.

There’s similarly no way to restructure things by producing the desired uniform value earlier, before the conditional expression. For appropriate type ‘t’, the coalgebra used for the anamorphism must have type:

coalg :: a -> Base t a

which in our case reduces to:

coalg :: a -> TF.FreeF ModelF a a

You’ll find that there’s simply no way to add another TF.Free constructor to the mix while satisfying the above type. So it seems that with an anamorphism (or apomorphism, which encounters the same problem) we’re limited to denoting a single probabilistic operation on any recursive call.

Encoding, Correctly

We thus need a recursion scheme that allows us to add multiple levels of the base functor at a time. The most appropriate scheme appears to me to be the futumorphism, which I also wrote about in Time Traveling Recursion Schemes.

(As Patrick Thomson pointed out in his sublime series on recursion schemes, both anamorphisms and apomorphisms are special cases of the futumorphism.)

The coalgebra used by a futumorphism has a different type than that used by an ana- or apomorphism, namely:

coalg :: a -> Base t (Free (Base t) a)

In our case, this is:

coalg :: a -> TF.FreeF ModelF a (Free (TF.FreeF ModelF a) a)

Note that here we’ll be able to use additional ‘TF.Free’ constructors inside other expressions involving the base functor. In Time Traveling Recursion Schemes I referred to this as “working with values that don’t exist yet, while pretending like they do” – but better would be to say that one is simply defining values to be produced during (co)recursion, using separate monadic code.

Here’s how we’d encode the CRP using a futumorphism, in pseudocode:

crp n a = futu coalg (1, <initial restaurant>) where
  coalg (customer, tables)
    | customer >= n = TF.Pure tables
    | otherwise =
        let p = <probability of seating customer at new table>
        in  TF.Free (BernoulliF p (\accept ->
              if   accept
              then pure (succ customer, <seat at new table>)
              else do
                res <- liftF (TF.Free (UniformF (\u ->
                         <seat amongst occupied tables using 'u'>
                       )))
                pure (succ customer, res)))

Note that recursive points are expressed under a ‘TF.Free’ constructor by returning a value (using ‘pure’) in the free monad itself. This effectively allows us to use more than one embedded language construct on each recursive call – as many as we want, as a matter of fact. The familiar ‘liftF’ function lifts each such expression into the free monad for us.

I mentioned in Time Traveling Recursion Schemes that this sort of thing can look a little bit nicer if you have the appropriate embedded language terms floating around. If we define the following:

uniform :: Free (TF.FreeF ModelF a) Double
uniform = liftF (TF.Free (UniformF id))

then we can use it to tidy things up a bit:

crp n a = futu coalg (1, <initial restaurant>) where
  coalg (customer, tables)
    | customer >= n = TF.Pure tables
    | otherwise =
        let p = <probability of seating customer at new table>
        in  TF.Free (BernoulliF p (\accept ->
              if   accept
              then pure (succ customer, <seat at new table>)
              else do
                u <- uniform
                let res = <seat amongst occupied tables using 'u'>
                pure (succ customer, res)))

In any case, the futumorphism gets us to a faithfully-encoded CRP. It allows us to express multiple probabilistic operations in every recursive call, which is what’s required here due to our use of conditional probabilities.

Alternative Encodings

Now. Recall that I mentioned the following:

A natural way to encode the process is to seat each arriving customer at a new table with the appropriate probability, and then, if it turns out he is to be sat at an occupied table, to do that with the appropriate conditional probability (i.e., conditional on the fact that he’s not going to be seated at a new table).

This is probably the most natural way to encode the process, and indeed, if we only have Bernoulli and uniform language terms (or beta, Gaussian, etc. in place of uniform – something that can at least be transformed to produce a uniform, in any case), this seems to be the best we can do. But it is not the only way to encode the CRP. If we have a language term corresponding to a categorical distribution, then we can instead choose between a new table and any of the occupied tables simultaneously using the unconditional probabilities for each.

Let’s adjust our ModelF functor, adding a language term corresponding to a categorical distribution. It will have as its parameter a list of probabilities, one for each possible outcome under consideration:

data ModelF r =
    BernoulliF Double (Bool -> r)
  | UniformF (Double -> r)
  | CategoricalF [Double] (Int -> r)
  deriving Functor

With this we’ll be able to encode the CRP using a mere anamorphism, as the following pseudocode describes:

crp n a = ana coalg (1, <initial restaurant>) where
  coalg (customer, tables)
    | customer >= n = TF.Pure tables
    | otherwise =
        let ps = <unconditional categorical probabilities>
        in  TF.Free (CategoricalF ps (\i ->
              if   i == 0
              then (succ customer, <seat at new table>)
              else (succ customer, <seat at occupied table 'i - 1'>)
            ))

Since here we only ever express a single probabilistic term during recursion, the “standard” pattern we’ve used previously applies here. But it’s worth noting that we could still employ the “unconditional, then conditional” approach using a categorical distribution – we’d just use the conditional probabilities to sample from the occupied tables directly, rather than doing it in more low-level fashion using the single uniform draw. Given an appropriate ‘categorical’ term, that would look more like:

crp n a = futu coalg (1, <initial restaurant>) where
  coalg (customer, tables)
    | customer >= n = TF.Pure tables
    | otherwise =
        let p = <probability of seating customer at new table>
        in  TF.Free (BernoulliF p (\accept ->
              if   accept
              then pure (succ customer, <seat at new table>)
              else do
                let ps = <conditional categorical probabilities>
                i <- categorical ps
                pure (succ customer, <seat at occupied table 'i'>)))

The recursive structure in this case is more complicated, requiring a futumorphism instead of an anamorphism, but typically the conditional probabilities are easier to compute.

Fin

So, some takeaways here, if one wants to indulge in this sort of framework:

If we want to express a stochastic process using multiple probabilistic operations in any given recursive call, we may need to employ a scheme that supports richer (co)recursion than a plain anamorphism or apomorphism. Here that’s captured nicely by a futumorphism, which naturally captures what we’re looking for.

The same might be true if our functor is sufficiently limited, as was the case here if we supported only the Bernoulli and uniform distributions. There we had no option but to express the recursion using condiitonal probabilistic operations, and so needed the richer recursive structure that a futumorphism provides.

On the other hand, it may not be the case that one needs the richer structure provided by a futumorphism, if instead one can express the coalgebra using only a single layer of the base functor. Adding a primitive categorical distribution to our embedded language eliminated the need to use conditional probabilities when describing the recursion, allowing us to drop back to a “basic” anamorphism.

Here is a gist containing a fleshed-out version of the code above, if you’d like to play with it. Enjoy!