17 Jan 2025
I wanted to make a quick addendum to my last post
in that I did some further experimenting with Data.ByteString.Builder
on both the base16 encoding and decoding tasks, comparing results with
the impure direct-allocation-and-write-based implementations I mentioned
previously.
I had remarked that builders can be pretty efficient if you’re careful
to pack your data aggressively, such that you don’t wind up needing to
use too many builders in the first place. I decided to try minimising,
as in objectively minimising, the number of builders required in both
base16 encoding & decoding, to see what kind of performance I could
squeeze out while sticking to the pure API. The builders didn’t
disappoint.

How would one “objectively minimise” the number of builders required
here? Simply by processing the biggest-sized chunk possible at a time,
given we always want to write a Word64. If we can’t do that, we’ll
write a Word32 and a Word16 and a Word8. If we can’t do that, we’ll
write a Word32 and a Word16. And so on. We can figure all this out
just by doing some checks on the length of the input bytestring when
starting out: we trade some additional cheap arithmetic operations
on machine integers up-front for fewer expensive builder allocations
further down the line.
For encoding, this means doing the following checks:
encode :: BS.ByteString -> BS.ByteString
encode bs@(BI.PS _ _ l)
| l < 64 = to_strict_small loop
| otherwise = to_strict loop
where
loop
| l `rem` 4 == 0 = go64 bs
| (l - 3) `rem` 4 == 0 = case BS.splitAt (l - 3) bs of
(chunk, etc) ->
go64 chunk
<> go32 (BU.unsafeTake 2 etc)
<> go16 (BU.unsafeDrop 2 etc)
| (l - 2) `rem` 4 == 0 = case BS.splitAt (l - 2) bs of
(chunk, etc) -> go64 chunk <> go32 etc
| (l - 1) `rem` 4 == 0 = case BS.splitAt (l - 1) bs of
(chunk, etc) -> go64 chunk <> go16 etc
| l `rem` 2 == 0 = go32 bs
| (l - 1) `rem` 2 == 0 = case BS.splitAt (l - 1) bs of
(chunk, etc) -> go32 chunk <> go16 etc
| otherwise = go16 bs
where each ‘go’ function writes words with the indicated number of bits
at a time, e.g.:
go64 b = case BS.splitAt 4 b of
(chunk, etc)
| BS.null chunk -> mempty
| otherwise ->
let !w16_0 = expand_w8 (BU.unsafeIndex chunk 0)
!w16_1 = expand_w8 (BU.unsafeIndex chunk 1)
!w16_2 = expand_w8 (BU.unsafeIndex chunk 2)
!w16_3 = expand_w8 (BU.unsafeIndex chunk 3)
!w64 = fi w16_0 `B.shiftL` 48
.|. fi w16_1 `B.shiftL` 32
.|. fi w16_2 `B.shiftL` 16
.|. fi w16_3
in BSB.word64BE w64 <> go64 etc
and where expand_w8 is just a variant of the previous ‘hilo’ function
that returns a Word16 directly, rather than a pair of Word8’s.
‘go32’ works on a chunk of size two, writing a single Word32, and ‘go16’
on a chunk of size one, writing a Word16. The point of having all these
functions is that we can now always write the largest-sized word that we
can, instead of writing Word8’s or Word16’s exclusively.
(Decoding works similarly, except we need more checks, and an additional
‘go8’ function to handle the one-byte case. I won’t paste the salad of
conditionals required here.)
In any case, by employing this strategy we can come pretty close to
the performance of the impure implementations. Here are some benchmark
results for encoding a 1kb input:
benchmarking encode/ppad-base16
time 5.929 μs (5.847 μs .. 6.013 μs)
0.999 R² (0.998 R² .. 0.999 R²)
mean 5.975 μs (5.913 μs .. 6.057 μs)
std dev 233.1 ns (172.4 ns .. 310.0 ns)
benchmarking encode/base16-bytestring
time 3.246 μs (3.233 μs .. 3.262 μs)
1.000 R² (1.000 R² .. 1.000 R²)
mean 3.284 μs (3.268 μs .. 3.303 μs)
std dev 61.05 ns (47.83 ns .. 76.77 ns)
benchmarking encode/base16
time 3.236 μs (3.221 μs .. 3.253 μs)
1.000 R² (1.000 R² .. 1.000 R²)
mean 3.244 μs (3.233 μs .. 3.256 μs)
std dev 37.31 ns (31.87 ns .. 47.21 ns)
Case Allocated GCs
ppad-base16 (encode) 53,704 0
base16-bytestring (encode) 2,272 0
base16 (encode) 2,256 0
We’re allocating 25x more than the impure versions, but are only 2x
slower or less. Here’s the decoding story:
benchmarking decode/ppad-base16
time 4.942 μs (4.884 μs .. 4.995 μs)
0.999 R² (0.998 R² .. 0.999 R²)
mean 4.908 μs (4.854 μs .. 4.964 μs)
std dev 176.8 ns (150.3 ns .. 214.3 ns)
variance introduced by outliers: 46% (moderately inflated)
benchmarking decode/base16-bytestring
time 540.8 ns (533.7 ns .. 548.2 ns)
0.999 R² (0.999 R² .. 0.999 R²)
mean 541.6 ns (536.9 ns .. 547.5 ns)
std dev 17.64 ns (13.87 ns .. 22.24 ns)
variance introduced by outliers: 47% (moderately inflated)
benchmarking decode/base16
time 555.8 ns (549.7 ns .. 560.9 ns)
0.999 R² (0.999 R² .. 1.000 R²)
mean 550.7 ns (546.7 ns .. 555.5 ns)
std dev 15.46 ns (13.11 ns .. 18.97 ns)
variance introduced by outliers: 39% (moderately inflated)
Case Allocated GCs
ppad-base16 (decode) 21,960 0
base16-bytestring (decode) 128 0
base16 (decode) 2,440 0
We’re allocating less (we’re writing less), but are closer to 10x
slower. Not too bad, all things considered!
(N.b., it’s worth noting that the impure decoding functions also use
what appears to be a more efficient lookup table to convert from
hex characters back to Word8, so that may account for some of the
differential there.)
16 Jan 2025
In this post I’m going to incrementally optimise a simple base16
(hexadecimal) encoding routine and illustrate what sort of performance
boost each optimisation yields. Hopefully it can be used to glean a bit
about what tends to make Haskell code fast – especially code that deals
with bytestrings.
You can think of this as a kind of supplement to Chris
Done’s Fast Haskell: Competing with C at parsing
XML post from
a few years ago. Here, like in Chris’s example, we’re going to focus
a lot on bytestring handling, though we’ll deal with some different
issues than he faced, and also eventually go a little lower-level on the
bytestring side of things.
Base16 Encoding
Let’s get right into it. The basic idea here is: for each byte
(Word8) in an input, extract its high and low bits, and then map each
(effectively a Word4) to a character from the hex alphabet:
import qualified Data.Bits as B
import qualified Data.ByteString as BS
hex_charset :: BS.ByteString
hex_charset = "0123456789abcdef"
hilo :: Word8 -> (Word8, Word8)
hilo b =
let hi = BS.index hex_charset (fromIntegral b `B.shiftR` 4)
lo = BS.index hex_charset (fromIntegral b .&. 0b00001111)
in (hi, lo)
You then get a base16-encoded output by gluing the resulting characters
together in the appropriate fashion:
encode :: BS.ByteString -> BS.ByteString
encode bs = go mempty 0
where
l = BS.length bs
go !acc j
| j == l = BS.reverse acc
| otherwise =
let (hi, lo) = hilo (BS.index bs j)
in go (BS.cons lo (BS.cons hi acc)) (succ j)
There are some things here that might stick out to someone
accustomed to writing performant Haskell code, but it’s an otherwise
reasonable-looking first take. How does it perform on a 1kb input?
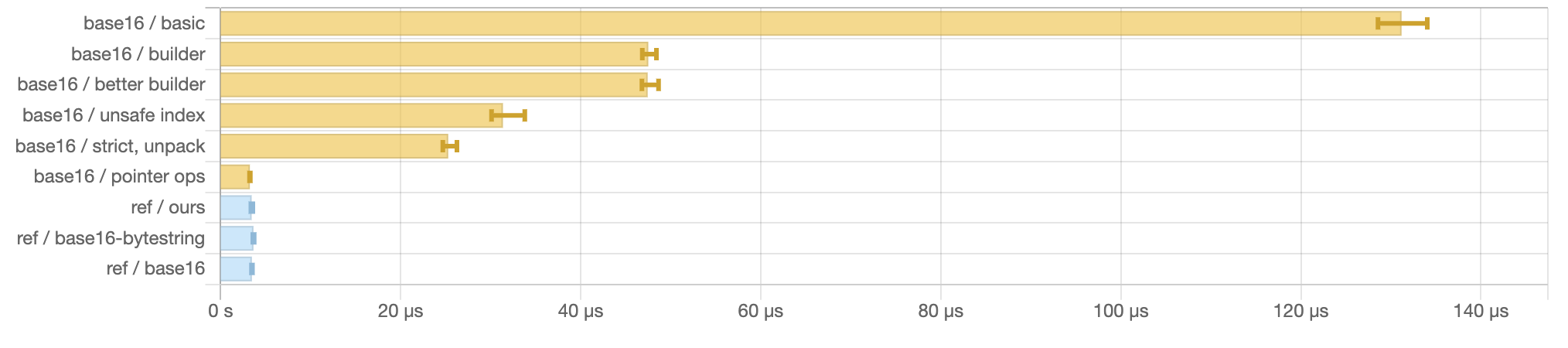
benchmarking base16/basic
time 114.2 μs (113.1 μs .. 115.4 μs)
0.999 R² (0.998 R² .. 1.000 R²)
mean 116.1 μs (115.1 μs .. 118.3 μs)
std dev 4.453 μs (2.609 μs .. 8.263 μs)
variance introduced by outliers: 38% (moderately inflated)
Allocated GCs
basic 2,326,160 0
Well, according to weigh it
seems to allocate a ton. The primary issue is that every invocation of
the ‘cons’ function creates a copy of its input bytestring; this is the
main thing that would scream out at an experienced Haskeller if they
were to glance at the above code. We’re not dealing with O(1) ‘cons’ in
bytestring-land, as we are when we use lists.
(As a side note: although ‘BS.reverse’ might raise an eyebrow, it’s
actually really fast. It’s a FFI call to a C reverse routine.)
Builders
A more efficient way to construct bytestrings is via
Data.ByteString.Builder, which supports constant-time concatenation of
sequences of bytes. Here’s a version of ‘encode’ that uses builders:
import qualified Data.ByteString.Builder as BSB
to_strict :: BSB.Builder -> BS.ByteString
to_strict = BS.toStrict . BSB.toLazyByteString
{-# INLINE to_strict #-}
encode :: BS.ByteString -> BS.ByteString
encode bs = to_strict (go 0)
where
l = BS.length bs
go j
| j == l = mempty
| otherwise =
let (hi, lo) = hilo (BS.index bs j)
in BSB.word8 hi <> BSB.word8 lo <> go (succ j)
There’s a new function to convert the builder back to a strict
bytestring, and now we concatenate builder singletons in order. Simple
enough. How does it compare in terms of performance?
benchmarking base16/builder
time 42.54 μs (42.01 μs .. 43.27 μs)
0.999 R² (0.999 R² .. 0.999 R²)
mean 42.88 μs (42.57 μs .. 43.22 μs)
std dev 1.105 μs (946.6 ns .. 1.387 μs)
variance introduced by outliers: 24% (moderately inflated)
Allocated GCs
builder 397,768 0
Much better. It allocates about 6x less and is almost 3x faster.
Builders are definitely worth knowing about when dealing with
bytestrings, as they’re easy to use, and allow one to write pure code
that performs reasonably well. There’s also some fine-tining you can do
in order to squeeze additional performance out of them in certain cases.
For small inputs, you can use a custom strategy to more efficiently
convert builders to lazy bytestrings en route to a strict one, e.g.:
import qualified Data.ByteString.Builder.Extra as BE
to_strict_small :: BSB.Builder -> BS.ByteString
to_strict_small = BS.toStrict
. BE.toLazyByteStringWith (BE.safeStrategy 128 BE.smallChunkSize) mempty
Using less builders helps as well, and probably even moreso. Consider
the following, in which the loop writes a single Word16 at a time
instead of two Word8’s:
encode :: BS.ByteString -> BS.ByteString
encode bs@(BI.PS _ _ l)
| l < 128 = to_strict_small (go 0)
| otherwise = to_strict (go 0)
where
go j
| j == l = mempty
| otherwise =
let (hi, lo) = hilo (BS.index bs j)
w16 = fromIntegral hi `B.shiftL` 8
.|. fromIntegral lo
in BSB.word16BE w16 <> go (succ j)
It allocates slightly less, and is a microsecond peppier, because
there’s just less building going on:
benchmarking base16/better builder
time 40.96 μs (40.64 μs .. 41.33 μs)
0.999 R² (0.999 R² .. 1.000 R²)
mean 41.12 μs (40.79 μs .. 41.48 μs)
std dev 1.163 μs (969.0 ns .. 1.494 μs)
variance introduced by outliers: 28% (moderately inflated)
Allocated GCs
better builder 389,592 0
(Note that I’ve also introduced the use of the ‘BI.PS’ pattern synonym
here, but only to more easily grab the input bytestring’s length. It has
nothing to do with performance.)
Unsafe Functions
Another easy gain can be won by replacing the calls to bytestring’s
‘index’ with its ‘unsafeIndex’ variant:
import qualified Data.ByteString.Unsafe as BU
hilo :: Word8 -> (Word8, Word8)
hilo b =
let hi = BU.unsafeIndex hex_charset (fromIntegral b `B.shiftR` 4)
lo = BU.unsafeIndex hex_charset (fromIntegral b .&. 0b00001111)
in (hi, lo)
encode :: BS.ByteString -> BS.ByteString
encode bs@(BI.PS _ _ l)
| l < 128 = to_strict_small (go 0)
| otherwise = to_strict (go 0)
where
go j
| j == l = mempty
| otherwise =
let (hi, lo) = hilo (BU.unsafeIndex bs j)
w16 = fromIntegral hi `B.shiftL` 8
.|. fromIntegral lo
in BSB.word16BE w16 <> go (succ j)
It often makes sense to do this so long as you can prove that the call
is actually safe (the compiler, of course, can’t), as ‘unsafeIndex’
reliably yields a decent performance boost. In this case, the unsafe
indexing into the hex alphabet in ‘hilo’ is being done with what are
effectively four-bit words, which will always be safe to use as indices
in a 16-length bytestring (there are 2^4 = 16 distinct Word4’s). The
unsafe index called in the body of the loop can similarly be verified
to remain safely within the input bytestring’s bounds, since the loop
terminates when its index argument hits the end.
The performance now:
benchmarking base16/unsafe index
time 25.58 μs (25.25 μs .. 25.89 μs)
0.998 R² (0.997 R² .. 0.999 R²)
mean 25.69 μs (25.41 μs .. 26.03 μs)
std dev 1.051 μs (852.3 ns .. 1.396 μs)
variance introduced by outliers: 47% (moderately inflated)
Allocated GCs
unsafe index 233,944 0
Another substantial win. Much less allocation and a great reduction in
wall-clock time.
Note however that not all unsafe functions will yield a boost as
impressive as bytestring’s ‘unsafeIndex’. I’ve never found the
‘unsafeShiftL’ and ‘unsafeShiftR’ functions in Data.Bits to ever really
seem to do much at all, for example, so we’ll keep the plain ‘B.shiftR’
call in ‘hilo’ above.
Unboxed Primitives
Next up is another optimisation that any seasoned Haskeller should know
about: use unboxed types, unless there’s some unusual reason not to.
Unboxed values require no allocation. To quote the GHC user
guide:
The representation of a Haskell Int, for example, is a two-word heap
object. An unboxed type, however, is represented by the value itself, no
pointers or heap allocation are involved.
Unboxed types correspond to the “raw machine” types you would use
in C: Int# (long int), Double# (double), Addr# (void *), etc.
The primitive operations (PrimOps) on these types are what you might
expect; e.g., (+#) is addition on Int#s, and is the machine-addition
that we all know and love—usually one instruction.
You can work with unboxed types and values explicitly by using the
appropriate imports and the MagicHash pragma, which can actually be
pretty nice, because you express what’s really going on, but more
commonly, unboxed types are denoted via strictness annotations and the
UNPACK pragma, like so:
data W8Pair = Pair
{-# UNPACK #-} !Word8
{-# UNPACK #-} !Word8
hilo :: Word8 -> W8Pair
hilo b =
let !hi = BU.unsafeIndex hex_charset (fromIntegral b `B.shiftR` 4)
!lo = BU.unsafeIndex hex_charset (fromIntegral b .&. 0b00001111)
in Pair hi lo
encode :: BS.ByteString -> BS.ByteString
encode bs@(BI.PS _ _ l)
| l < 128 = to_strict_small (go 0)
| otherwise = to_strict (go 0)
where
go j
| j == l = mempty
| otherwise =
let !(Pair hi lo) = hilo (BU.unsafeIndex bs j)
in BSB.word8 hi <> BSB.word8 lo <> go (succ j)
Now ‘hilo’ as a whole – so long as one compiles with optimisation
– simply doesn’t allocate at all, and the overall allocation and
wall-clock time are trimmed by a decent chunk yet again:
benchmarking base16/strict, unpack
time 20.90 μs (20.56 μs .. 21.25 μs)
0.998 R² (0.998 R² .. 0.999 R²)
mean 20.97 μs (20.76 μs .. 21.19 μs)
std dev 742.1 ns (619.9 ns .. 938.1 ns)
variance introduced by outliers: 41% (moderately inflated)
Allocated GCs
strict, unpack 176,600 0
At this point the allocation is absolutely dominated by the builders, so
if we want to do better we’ll need to do something about them.
Direct Allocation and Writes
A strict ByteString is just a wrapper around some memory. It’s defined
in recent versions via:
data ByteString = BS
{-# UNPACK #-} !(ForeignPtr Word8) -- payload
{-# UNPACK #-} !Int -- length
So, a “foreign pointer” to some memory location and a length (where a
foreign pointer means a pointer to something that isn’t managed by the
RTS in the same way normal data is). To most efficiently create a
bytestring, one can thus do it in the same way one would do so in C:
allocate some memory and write to it directly.
This is the line beyond which one probably can’t consider his code
to be “pure Haskell” anymore. An ‘unsafePerformIO’ call or similar
isn’t technically going to be required (it could be masked via
‘Data.ByteString.Internal.unsafeCreate’, for example), and one still
doesn’t need to type the {-# LANGUAGE FFI #-} pragma at the top of his
module. But it’s safe to say that any assertions of purity would at this
point be at least somewhat controversial.
But if one does want to wield this particular Ring of Power, it
can be done like so (this is basically what Bryan O’Sullivan’s
base16-bytestring or Emily Pillmore’s base16 package do, for example):
import Foreign.Ptr
import Foreign.Storable
import GHC.ForeignPtr
import GHC.Word
import System.IO.Unsafe
encode :: BS.ByteString -> BS.ByteString
encode (BI.PS bs _ l) = unsafeDupablePerformIO $ do
buffer <- mallocPlainForeignPtrBytes (l * 2)
withForeignPtr buffer $ \p_buf ->
withForeignPtr bs $ \p_src ->
go p_buf p_src (p_src `plusPtr` l)
pure (BI.BS buffer (l * 2))
where
go !buf !src !end
| src == end = pure ()
| otherwise = do
!b <- peek src
let !(Pair hi lo) = hilo b
poke buf hi
poke (buf `plusPtr` 1) lo
go (buf `plusPtr` 2) (src `plusPtr` 1) end
Here we allocate a buffer explicitly and loop through the input
bytestring’s allocated memory, rather than its Haskell representation,
in order to populate it, wrapping the result up in a new bytestring via
the raw ‘BI.BS’ constructor. It’s worth noting that we could still just
make use of ‘unsafeIndex’ on the input bytestring if we wanted, rather
than making direct use of its foreign pointer, but since we’re already
going big, why not go all the way?
This function allocates minimally, and indeed is at parity with the
relevant “encode” functions found in both the base16 and
base16-bytestring packages in terms of wall-clock time. It’s about 50x faster than the
initial naïve version, and perhaps 5x faster than the most efficient
version that used builders:
benchmarking base16/pointer ops
time 2.929 μs (2.903 μs .. 2.959 μs)
1.000 R² (0.999 R² .. 1.000 R²)
mean 2.950 μs (2.936 μs .. 2.967 μs)
std dev 52.87 ns (43.32 ns .. 64.89 ns)
variance introduced by outliers: 18% (moderately inflated)
Allocated GCs
pointer ops 120 0
I’m guessing this is probably about as fast as one can make this
function via “normal” means. Other techniques that I tried while
preparing this article don’t seem to move the needle much on this
problem, if at all. I’d be pretty impressed by anything that produced
another order-of-magnitude performance boost, though – if anyone can
achieve that, I’d love to hear about it!
Recap
So to conclude with a quick, advice-laden summary of the techniques used
here:
-
Avoid using BS.cons, BS.append, and so on, as each requires making a
copy of their input bytestring or bytestrings. Instead, prefer
builders, and try to pack your data so that you can get away with as
few of them as possible. If you can write an occasional Word64, that’s
much better than writing many Word8’s.
It’s worth nothing, though, that occasional uses of cons, append, etc.
on small inputs can be very benign, and even hard to beat by clever
rewriting. You don’t always need to reach for builders or
harder-core optimisations every time you want to glue a few bytestrings
together. Consider this HMAC implementation from
ppad-sha256:
hmac
:: BS.ByteString
-> BS.ByteString
-> BS.ByteString
hmac mk@(BI.PS _ _ l) text =
let step1 = k <> BS.replicate (64 - lk) 0x00
step2 = BS.map (B.xor 0x36) step1
step3 = step2 <> text
step4 = hash step3
step5 = BS.map (B.xor 0x5C) step1
step6 = step5 <> step4
in hash step6
where
!(KeyAndLen k lk)
| l > 64 = KeyAndLen (hash mk) 32
| otherwise = KeyAndLen mk l
It looks like there’s a lot of unnecessary copying going on here,
but in the grand scheme of things, it’s simply not that much, and
the bytestring functions are highly optimised, after all. I wasn’t
able to improve this function’s performance either by builders or
even low-level allocations and writes, including manually minimising
allocations, reusing memory areas, and so on. The story would be
different if I were calling these functions many times in a loop,
though, at which point builders or direct writes would definitely
prove useful.
-
Don’t necessarily shy away from unsafe functions if said use can be
proven to be perfectly safe. Aside from ‘unsafeIndex’, other things can
be useful, particularly ‘unsafeTake’ and ‘unsafeDrop’. These can
provide great performance boosts, though if one is not gunning for
absolute, maximum performance, then sure, it might be better to avoid
them.
It’s also worth nothing that there are some useful unsafe functions
that don’t exist in the bytestring API, but that can be assembled
manually. Take this home-cooked unsafe splitAt, for example, that does
no bounds checking:
data SSPair = SSPair
{-# UNPACK #-} !BS.ByteString
{-# UNPACK #-} !BS.ByteString
unsafe_splitAt :: Int -> BS.ByteString -> SSPair
unsafe_splitAt n (BI.BS x l) =
SSPair (BI.BS x n) (BI.BS (plusForeignPtr x n) (l - n))
-
Make data strict unless you for some reason need it to be lazy, and
always unpack strict fields when it’s possible to do so. You can also
use -funbox-strict-fields or -funbox-small-strict-fields to unbox
all strict fields at the module level, though I generally prefer the
more explicit local use of UNPACK pragmas.
-
Don’t be afraid to use low-level allocation and writes where it makes
sense to do so. It may be unnecessary, even in
highly-optimised library code (I chose to use builders in
ppad-bech32 because we’re never
dealing with large outputs there, for example), but it’s a great
technique to have around for when performance really counts.
If you’d like to play with the code yourself, I’ve pushed it to this
GitHub repo. Presuming you have
flake support enabled, you can use ‘nix develop’ to enter a Nix shell,
and then e.g. ‘cabal repl’ to open GHCi, or ‘cabal bench’ to run the
benchmark suite. Enjoy!
21 Dec 2024
(UPDATE 2026/02/06: the nukes were redeployed; I rode the bomb down
whooping, Major Kong style.)
I nuked all of my social media accounts years ago and never looked back.
My general take is that all legacy web 2.0-style social media stuff
needs to be ground under a boot, and then the boot filled with cement
and sank to the bottom of a particularly deep ocean. Just in case.
That said, I recently recreated an account on X using my old handle,
@jaredtobin (some other dude has nabbed
@jtobin, unfortunately), and will be experimenting with it for
traditional microblogging purposes for things that don’t warrant a full
post on this, my trusty long-form blog.
Why not nostr, etc.? Well, I could. I like nostr, and maybe I’ll mirror
my stuff there just for the lulz. But, pragmatically, X appears to
be where the action is, and I want my stuff to be easy to access and
interact with.
It’s an experiment. I’m aloof by nature, so there’s no guarantee I won’t
at some point turn up my nose and redeploy the nukes. But we’ll see how
it goes. Follow me there, if you’re into that kind of thing!

