Sorting Slower with Style

I previously wrote about implementing merge sort using recursion schemes. By using a hylomorphism we could express the algorithm concisely and true to its high-level description.

Insertion sort can be implemented in a similar way - this time by putting one recursion scheme inside of another.

Read on for details.

Apomorphisms

These guys don’t seem to get a lot of love in the recursion scheme tutorial du jour, probably because they might be the first scheme you encounter that looks truly weird on first glance. But apo is really not bad at all - I’d go so far as to call apomorphisms straightforward and practical.

So: if you remember your elementary recursion schemes, you can say that apo is to ana as para is to cata. A paramorphism gives you access to a value of the original input type at every point of the recursion; an apomorphism lets you terminate using a value of the original input type at any point of the recursion.

This is pretty useful - often when traversing some structure you just want to bail out and return some value on the spot, rather than continuing on recursing needlessly.

A good introduction is the toy ‘mapHead’ function that maps some other function over the head of a list and leaves the rest of it unchanged. Let’s first rig up a hand-rolled list type to illustrate it on:

{-# LANGUAGE DeriveFunctor #-}
{-# LANGUAGE TypeFamilies #-}

import Data.Functor.Foldable

data ListF a r =
    ConsF a r
  | NilF
  deriving (Show, Functor)

type List a = Fix (ListF a)

fromList :: [a] -> List a
fromList = ana coalg . project where
  coalg Nil        = NilF
  coalg (Cons h t) = ConsF h t

(I’ll come back to the implementation of ‘fromList’ later, but for now you can see it’s implemented via an anamorphism.)

Example One

Here’s ‘mapHead’ for our hand-rolled list type, implemented via apo:

mapHead :: (a -> a) -> List a -> List a
mapHead f = apo coalg . project where
  coalg NilF        = NilF
  coalg (ConsF h t) = ConsF (f h) (Left t)

Before I talk you through it, here’s a trivial usage example:

> fromList [1..3]
Fix (ConsF 1 (Fix (ConsF 2 (Fix (ConsF 3 (Fix NilF))))))
> mapHead succ (fromList [1..3])
Fix (ConsF 2 (Fix (ConsF 2 (Fix (ConsF 3 (Fix NilF))))))

Now. Take a look at the coalgebra involved in writing ‘mapHead’. It has the type ‘a -> Base t (Either t a)’, which for our hand-rolled list case simplifies to ‘a -> ListF a (Either (List a) a)’.

Just as a reminder, you can check this in GHCi using the ‘:kind!’ command:

> :set -XRankNTypes
> :kind! forall a. a -> Base (List a) (Either (List a) a)
forall a. a -> Base (List a) (Either (List a) a) :: *
= a -> ListF a (Either (List a) a)

So, inside any base functor on the right hand side we’re going to be dealing with some ‘Either’ values. The ‘Left’ branch indicates that we’re going to terminate the recursion using whatever value we pass, whereas the ‘Right’ branch means we’ll continue recursing as per normal.

In the case of ‘mapHead’, the coalgebra is saying:

• deconstruct the list; if it has no elements just return an empty list
• if the list has at least one element, return the list constructed by prepending ‘f h’ to the existing tail.

Here the ‘Left’ branch is used to terminate the recursion and just return the existing tail on the spot.

Example Two

That was pretty easy, so let’s take it up a notch and implement list concatenation:

cat :: List a -> List a -> List a
cat l0 l1 = apo coalg (project l0) where
  coalg NilF = case project l1 of
    NilF      -> NilF
    ConsF h t -> ConsF h (Left t)

  coalg (ConsF x l) = case project l of
    NilF      -> ConsF x (Left l1)
    ConsF h t -> ConsF x (Right (ConsF h t))

This one is slightly more involved, but the principles are almost entirely the same. If both lists are empty we just return an empty list, and if the first list has at most one element we return the list constructed by jamming the second list onto it. The ‘Left’ branch again just terminates the recursion and stops everything there.

If both lists are nonempty? Then we actually do some work and recurse, which is what the ‘Right’ branch indicates.

So hopefully you can see there’s nothing too weird going on - the coalgebras are really simple once you get used to the Either constructors floating around in there.

Paramorphisms involve an algebra that gives you access to a value of the original input type in a pair - a product of two values. Since apomorphisms are their dual, it’s no surprise that you can give them a value of the original input type using ‘Either’ - a sum of two values.

Insertion Sort

So yeah, my favourite example of an apomorphism is for implementing the ‘inner loop’ of insertion sort, a famous worst-case \(O(n^2)\) comparison-based sort. Granted that insertion sort itself is a bit of a toy algorithm, but the pattern used to implement its internals is pretty interesting and more broadly applicable.

This animation found on Wikipedia illustrates how insertion sort works:

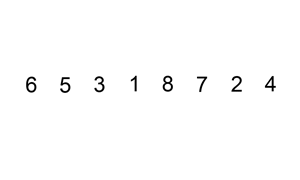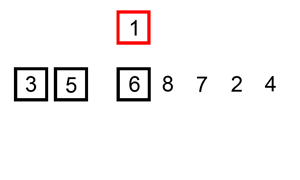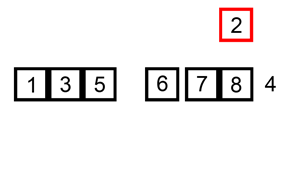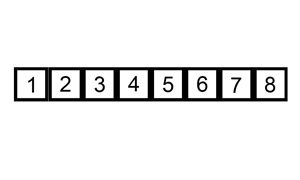
We’ll actually be doing this thing in reverse - starting from the right-hand side and scanning left - but here’s the inner loop that we’ll be concerned with: if we’re looking at two elements that are out of sorted order, slide the offending element to where it belongs by pushing it to the right until it hits either a bigger element or the end of the list.

As an example, picture the following list:

[3, 1, 1, 2, 4, 3, 5, 1, 6, 2, 1]

The first two elements are out of sorted order, so we want to slide the 3 rightwards along the list until it bumps up against a larger element - here that’s the 4.

The following function describes how to do that in general for our hand-rolled list type:

coalg NilF        = NilF
coalg (ConsF x l) = case project l of
  NilF          -> ConsF x (Left l)
  ConsF h t
    | x <= h    -> ConsF x (Left l)
    | otherwise -> ConsF h (Right (ConsF x t))

It says:

• deconstruct the list; if it has no elements just return an empty list
• if the list has only one element, or has at least two elements that are in sorted order, terminate with the original list by passing the tail of the list in the ‘Left’ branch
• if the list has at least two elements that are out of sorted order, swap them and recurse using the ‘Right’ branch

And with that in place, we can use an apomorphism to put it to work:

knockback :: Ord a => List a -> List a
knockback = apo coalg . project where
  coalg NilF        = NilF
  coalg (ConsF x l) = case project l of
    NilF          -> ConsF x (Left l)
    ConsF h t
      | x <= h    -> ConsF x (Left l)
      | otherwise -> ConsF h (Right (ConsF x t))

Check out how it works on our original list, slotting the leading 3 in front of the 4 as required. I’ll use a regular list here for readability:

> let test = [3, 1, 1, 2, 4, 3, 5, 1, 6, 2, 1]
> knockbackL test
[1, 1, 2, 3, 4, 3, 5, 1, 6, 2, 1]

Now to implement insertion sort we just want to do this repeatedly like in the animation above.

This isn’t something you’d likely notice at first glance, but check out the type of ‘knockback . embed’:

> :t knockback . embed
knockback . embed :: Ord a => ListF a (List a) -> List a

That’s an algebra in the ‘ListF a’ base functor, so we can drop it into cata:

insertionSort :: Ord a => List a -> List a
insertionSort = cata (knockback . embed)

And voila, we have our sort.

If it’s not clear how the thing works, you can visualize the whole process as working from the back of the list, knocking back unsorted elements and recursing towards the front like so:

[]
[1]
[2, 1] -> [1, 2]
[6, 1, 2] -> [1, 2, 6]
[1, 1, 2, 6]
[5, 1, 1, 2, 6] -> [1, 1, 2, 5, 6]
[3, 1, 1, 2, 5, 6] -> [1, 1, 2, 3, 5, 6]
[4, 1, 1, 2, 3, 5, 6] -> [1, 1, 2, 3, 4, 5, 6]
[2, 1, 1, 2, 3, 4, 5, 6] -> [1, 1, 2, 2, 3, 4, 5, 6]
[1, 1, 1, 2, 2, 3, 4, 5, 6]
[1, 1, 1, 1, 2, 2, 3, 4, 5, 6]
[3, 1, 1, 1, 1, 2, 2, 3, 4, 5, 6] -> [1, 1, 1, 1, 2, 2, 3, 3, 4, 5, 6]
[1, 1, 1, 1, 2, 2, 3, 3, 4, 5, 6]

Wrapping Up

And that’s it! If you’re unlucky you may be sorting asymptotically worse than if you had used mergesort. But at least you’re doing it with style.

The ‘mapHead’ and ‘cat’ examples come from the unreadable Vene and Uustalu paper that first described apomorphisms. The insertion sort example comes from Tim Williams’s excellent recursion schemes talk.

As always, I’ve dumped the code for this article into a gist.

Addendum: Using Regular Lists

You’ll note that the ‘fromList’ and ‘knockbackL’ functions above operate on regular Haskell lists. The short of it is that it’s easy to do this; recursion-schemes defines a data family called ‘Prim’ that basically endows lists with base functor constructors of their own. You just need to use ‘Nil’ in place of ‘[]’ and ‘Cons’ in place of ‘(:)’.

Here’s insertion sort implemented in the same way, but for regular lists:

knockbackL :: Ord a => [a] -> [a]
knockbackL = apo coalg . project where
  coalg Nil        = Nil
  coalg (Cons x l) = case project l of
    Nil           -> Cons x (Left l)
    Cons h t
      | x <= h    -> Cons x (Left l)
      | otherwise -> Cons h (Right (Cons x t))

insertionSortL :: Ord a => [a] -> [a]
insertionSortL = cata (knockbackL . embed)