Monadic Recursion Schemes

I have another few posts that I’d like to write before cluing up the whole recursion schemes kick I’ve been on. The first is a simple note about monadic versions of the schemes introduced thus far.

In practice you often want to deal with effectful versions of something like cata. Take a very simple embedded language, for example (“Hutton’s Razor”, with variables):

{-# LANGUAGE DeriveFunctor #-}
{-# LANGUAGE DeriveFoldable #-}
{-# LANGUAGE DeriveTraversable #-}
{-# LANGUAGE LambdaCase #-}

import           Control.Monad              ((<=<), liftM2)
import           Control.Monad.Trans.Class  (lift)
import           Control.Monad.Trans.Reader (ReaderT, ask, runReaderT)
import           Data.Functor.Foldable      hiding (Foldable, Unfoldable)
import qualified Data.Functor.Foldable      as RS (Foldable, Unfoldable)
import           Data.Map.Strict            (Map)
import qualified Data.Map.Strict            as Map

data ExprF r =
    VarF String
  | LitF Int
  | AddF r r
  deriving (Show, Functor, Foldable, Traversable)

type Expr = Fix ExprF

var :: String -> Expr
var = Fix . VarF

lit :: Int -> Expr
lit = Fix . LitF

add :: Expr -> Expr -> Expr
add a b = Fix (AddF a b)

(Note: Make sure you import ‘Data.Functor.Foldable.Foldable’ with a qualifier because GHC’s ‘DeriveFoldable’ pragma will become confused if there are multiple ‘Foldables’ in scope.)

Take proper error handling over an expression of type ‘Expr’ as an example; at present we’d have to write an ‘eval’ function as something like

eval :: Expr -> Int
eval = cata $ \case
  LitF j   -> j
  AddF i j -> i + j
  VarF _   -> error "free variable in expression"

This is a bit of a non-starter in a serious or production implementation, where errors are typically handled using a higher-kinded type like ‘Maybe’ or ‘Either’ instead of by just blowing up the program on the spot. If we hit an unbound variable during evaluation, we’d be better suited to return an error value that can be dealt with in a more appropriate place.

Look at the algebra used in ‘eval’; what would be useful is something like

monadicAlgebra = \case
  LitF j   -> return j
  AddF i j -> return (i + j)
  VarF v   -> Left (FreeVar v)

data Error =
    FreeVar String
  deriving Show

This won’t fly with cata as-is, and recursion-schemes doesn’t appear to include any support for monadic variants out of the box. But we can produce a monadic cata - as well as monadic versions of the other schemes I’ve talked about to date - without a lot of trouble.

To begin, I’ll stoop to a level I haven’t yet descended to and include a commutative diagram that defines a catamorphism:

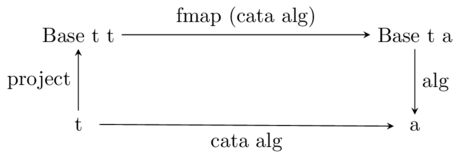
To read it, start in the bottom left corner and work your way to the bottom right. You can see that we can go from a value of type ‘t’ to one of type ‘a’ by either applying ‘cata alg’ directly, or by composing a bunch of other functions together.

If we’re trying to define cata, we’ll obviously want to do it in terms of the compositions:

cata:: (RS.Foldable t) => (Base t a -> a) -> t ->  a
cata alg = alg . fmap (cata alg) . project

Note that in practice it’s typically more efficient to write recursive functions using a non-recursive wrapper, like so:

cata:: (RS.Foldable t) => (Base t a -> a) -> t ->  a
cata alg = c where c = alg . fmap c . project

This ensures that the function can be inlined. Indeed, this is the version that recursion-schemes uses internally.

To get to a monadic version we need to support a monadic algebra - that is, a function with type ‘Base t a -> m a’ for appropriate ‘t’. To translate the commutative diagram, we need to replace ‘fmap’ with ‘traverse’ (requiring a ‘Traversable’ instance) and the final composition with monadic (or Kleisli) composition:

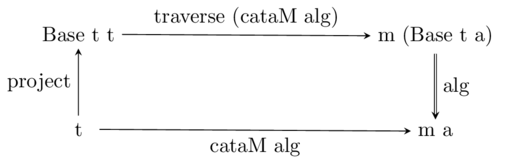
The resulting function can be read straight off the diagram, modulo additional constraints on type variables. I’ll go ahead and write it directly in the inline-friendly way:

cataM
  :: (Monad m, Traversable (Base t), RS.Foldable t)
  => (Base t a -> m a) -> t ->  m a
cataM alg = c where
  c = alg <=< traverse c . project

Going back to the previous example, we can now define a proper ‘eval’ as follows:

eval :: Expr -> Either Error Int
eval = cataM $ \case
  LitF j   -> return j
  AddF i j -> return (i + j)
  VarF v   -> Left (FreeVar v)

This will of course work for any monad. A common pattern on an ‘eval’ function is to additionally slap on a ‘ReaderT’ layer to supply an environment, for example:

eval :: Expr -> ReaderT (Map String Int) (Either Error) Int
eval = cataM $ \case
  LitF j   -> return j
  AddF i j -> return (i + j)
  VarF v   -> do
    env <- ask
    case Map.lookup v env of
      Nothing -> lift (Left (FreeVar v))
      Just j  -> return j

And just an example of how that works:

> let open = add (var "x") (var "y")
> runReaderT (eval open) (Map.singleton "x" 1)
Left (FreeVar "y")
> runReaderT (eval open) (Map.fromList [("x", 1), ("y", 5)])
Right 6

You can follow the same formula to create the other monadic recursion schemes. Here’s monadic ana:

anaM
  :: (Monad m, Traversable (Base t), RS.Unfoldable t)
  => (a -> m (Base t a)) -> a -> m t
anaM coalg = a where
  a = (return . embed) <=< traverse a <=< coalg

and monadic para, apo, and hylo follow in much the same way:

paraM
  :: (Monad m, Traversable (Base t), RS.Foldable t)
  => (Base t (t, a) -> m a) -> t -> m a
paraM alg = p where
  p   = alg <=< traverse f . project
  f t = liftM2 (,) (return t) (p t)

apoM
  :: (Monad m, Traversable (Base t), RS.Unfoldable t)
  => (a -> m (Base t (Either t a))) -> a -> m t
apoM coalg = a where
  a = (return . embed) <=< traverse f <=< coalg
  f = either return a

hyloM
  :: (Monad m, Traversable t)
  => (t b -> m b) -> (a -> m (t a)) -> a -> m b
hyloM alg coalg = h
  where h = alg <=< traverse h <=< coalg

These are straightforward extensions from the basic schemes. A good exercise is to try putting together the commutative diagrams corresponding to each scheme yourself, and then use them to derive the monadic versions. That’s pretty fun to do for para and apo in particular.

If you’re using these monadic versions in your own project, you may want to drop them into a module like ‘Data.Functor.Foldable.Extended’ as recommended by my colleague Jasper Van der Jeugt. Additionally, there is an old issue floating around on the recursion-schemes repo that proposes adding them to the library itself. So maybe they’ll turn up in there eventually.